- Цветы и растения
- Аквариум и рыбы
- Для работы
- Для сайта
- Для обучения
- Почтовые индексы Украины
- Всяко-разно
- Электронные библиотеки
- Реестры Украины
- Старинные книги о пивоварении
- Словарь старославянских слов
- Все романы Пелевина
- 50 книг для детей
- Стругацкие, сочинения в 33 томах
- Записи Леонардо да Винчи
- Биология поведения человека
Главная  Экономика Экономика  Книги Книги  Зовнішньоекономічна політика - Храмов В.О. Зовнішньоекономічна політика - Храмов В.О. |
Зовнішньоекономічна політика - Храмов В.О.
Вибір довгострокової політики у демократичній системі
У демократичній двопартійній системі правляча партія періодично переобирається, причому критерієм перемоги на виборах у
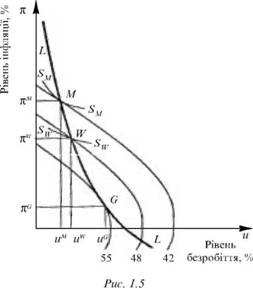
вітчизняній простій моделі є діаграма, зображена на рис. 1.4. Партія, яка перебуває при владі, змушена здійснювати політику, що визначається короткостроковою "кривою Філліпса", і водночас враховувати, що стан економіки, якому виборець надає найбільшу перевагу і за яким він судить про ефективність уряду, на рис. 1.4 розміщені в лівому куті діаграми, де рівні інфляції й безробіття мінімальні. Управління економікою в період між виборами має забезпечити отримання більшості голосів на наступних виборах, причому як уряд, так і електорат цілком усвідомлюють, що це означає. Таке знання їм так само забезпечує діаграма, зображена на рис. 1.4.
Прагнення узгодити політичні та економічні цілі можна проілюструвати за допомогою діаграми, зображеної на рис. 1.6.
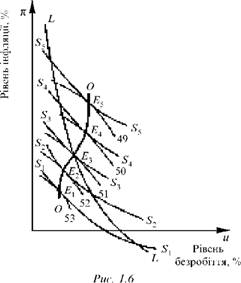
Припустимо, що правляча партія змушена дотримуватись політики, що зображена короткостроковою кривою (рис. 1.6). Щоб зібрати максимальну кількість голосів на виборах, політика правлячої партії має відповідати точці дотику Е1 цієї кривої з однією з кривих ФЗГ. У такому разі це буде 53%-ва крива ФЗГ, тобто, дотримуючись такої економічної політики, партія може розраховувати на перемогу на виборах.
Ця ситуація цілком аналогічна тій, що виникає під час аналізу кривих байдужості у звичайній теорії граничної корисності, коли максимальне задоволення за заданим бюджетним обмеженням досягається у випадку дотику кривої байдужості до бюджетної прямої. Роль бюджетного обмеження в цьому разі відіграють криві ФЗГ.
Повторюючи таке міркування, можна отримати набір точок Е1, Е2,..., Е5 на рис. 1.6, кожна з яких відповідає максимально досяжному ефекту на виборах. Якщо з'єднати ці точки, отримаємо безперервну криву 00, яку можна назвати кривою ефективної передвиборної стратегії (ЕПС).
Подивимось, що станеться, коли за цільову стратегію вибрано точку Е1. Вона розміщена на короткостроковій кривій S1S1 дещо лівіше від довгострокової кривої ЬЬ, що, як відомо, має зумовлювати безперервний перехід на дедалі вищі короткострокові криві і — за оптимальної стратегії — руху вгору кривою ЕПС. При цьому політика правлячої партії в разі потреби стає дедалі менш популярною, бо призводить до підвищення рівнів безробіття та інфляції.
Якби початково було вибрано точку Е5, то рух кривою 00 відбувався б у зворотному напрямі, тобто вниз. В обох випадках стійким є положення в точці Е3, де крива 00 (ЕПС) перетинає довго-
строкову "криву Філліпса". Докладніше ситуацію, що виникла, ілюструє рис. 1.7.
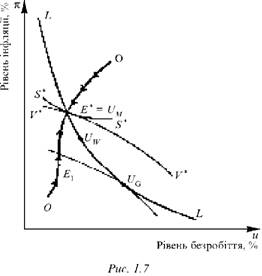
Положення рівноваги Е* є точкою перетину чотирьох кривих: довгострокової "кривої Філліпса" ЬЬ, кривої 00 (ЕПС), короткострокової "кривої Філліпса" S*S* і кривої V*V*(ФЗГ). Останні дві криві в цій точці стикаються, а це, як відомо (див. рис. 1.5), є ознакою суто егоїстичної політики, що не враховує переваг майбутніх поколінь.
Іншими словами, у демократичній системі, де соціальна політика визначається шляхом загальних виборів, цільова програма правлячої партії виявляється егоїстичною, рівень інфляції вищий, а рівень безробіття нижчий за оптимальні значення цих показників, що відповідають точці Uw на рис. 1.7.
Поведінка в короткостроковому періоді: політичний діловий цикл
Отже, економічна система досягає стану рівноваги в точці Е* = = Eм. При цьому, однак, не було враховано кінцевого періоду перебування при владі правлячої партії. Можливість зміни правління шляхом демократичних виборів вносить істотну корективу в цю довгострокову схему. Нагадаємо, що ця система в розглядуваній моделі описується ФЗГ g(ut, nt), зображеною на рис. 1.4 контурами еквівідсоткових кривих, що вказують відсоток голосуючих, що схвалюють поєднання рівнів інфляції п( і безробіття иt.. Крім того, система відбиває ставлення суспільства і правлячої партії, яка є виразником цього ставлення, до багатства, нагромадженого суспільством, до його ресурсів, для чого вводиться функція ФСД W у вигляді інтеграла від ФЗГ з дисконтуючим множником, що відбиває ставлення нинішнього покоління до майбутніх. На основі виконаного дослідження доходимо висновку, що уряд, не обмежений у часі, завжди здійснює егоїстичну політику, яка абсолютно не враховує майбутніх поколінь.
Як можна передбачити кінець правління однієї партії і можливість її заміни іншою в межах моделі В. Нордхауса? Він вважає, що, розглядаючи розвиток економічної системи в короткостроковому періоді, потрібно передусім брати до уваги наявність у людей пам'яті про минулі події, принаймні в межах електорального періоду 0. На момент настання виборів ця пам'ять має загострюватись, посилюючи негативний нюанс, викликаний поточним правлінням. Іншими словами, статична функція голосування g(u, п) має бути замінена динамічною, яку з огляду на наведені міркування можна записати у вигляді інтеграла:
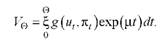
Проте експонента, що "загострює" пам'ять, продовжує діяти у тому ж егоїстичному ключі, охоплюючи лише електоральний період тривалістю 0. Вплив цього "меморіально-загострюючого" чинника m, (раніше працював "довгограючий", довгостроковий дисконтую-чий чинник р) на економічну політику істотно відрізняється від впливу чинника р. Цю відмінність наочно ілюструє рис. 1.8.
Тоді як дисконтуючий чинник ехр(-р.) діяв від початку періоду з дедалі меншою силою (крива ОЕ), "загострюючий" чинник ехр( mt) діяв з наростаючою силою, але лише впродовж електорального періоду 0, причому його максимум припав на момент наступних виборів, після чого пам'ять сягнула нуля (крива FABC). Після виборів усе повторюється.
Формально політика правлячої партії перебуває в оптимізації введеної функції Vе, що є інтегралом від ФЗГ g(ut, п(), яка, як зазначалося, залежить від рівнів інфляції п( і безробіття ut. Теорія цієї залежності накладає макроекономічні обмеження на "криву Філліпса", які виражаються такою парою функціональних рівнянь:
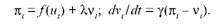
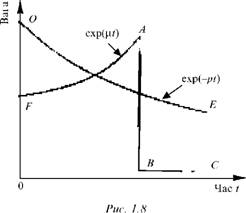
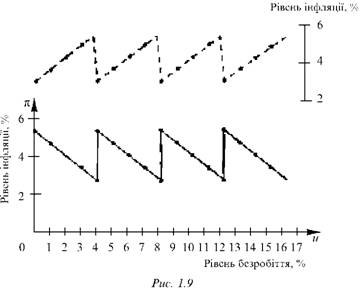
Відомі рівні безробіття и( і реальної інфляції рt доповнює очікувана інфляція pt і з другого рівняння (диференціального) випливає, що швидкість підвищення очікуваного рівня інфляції пропорційна різниці, яка існує на цей момент між реальністю та очікуваннями. Крім того, у наведених рівняннях є коефіцієнти пропорційності X і у, які можна варіювати, досліджуючи поведінку "кривої Філліпса", що залежить від часу. Обидва рівняння є основою стандартної теорії цієї кривої, найбільший внесок у розвиток якої зробив Е. Фелпс [71].
Отже, завдання, яке поставив і розв'язав В. Нордхаус, формально зводиться до визначення максимальних значень інтеграла Vв, що є функцією голосування у короткострокових (електоральних) періодах за обмежень, накладених на підінтегральний вираз рівняннями Е. Фелпса. Метод розв'язання таких задач добре розроблений, хоча йому притаманні аналітичні тонкощі і потрібна математична підготовка. Втішно, що в результаті складних обчислень В. Нордха-усу вдалося отримати цілком відчутний кінцевий результат, графічно показаний на рис. 1.9.
Цей результат можна інтерпретувати так. Всередині електорального циклу правляча партія, яка здобула перемогу на виборах, в першу половину періоду свого правління здійснює жорстку політику "батога", усіма силами придушуючи інфляцію, що супроводжується підвищенням рівня безробіття. Друга половина періоду правління позначується обдаровуванням "пряниками": зусилля витрачаються
на зниження рівня безробіття незважаючи на підвищення рівня інфляції. У подальшому незалежно від того, яка партія переможе на наступних виборах, повторюється той самий цикл, тобто дві стадії — "батога" і "пряника". При цьому політика завжди залишається егоїстичною в тому розумінні, що враховуються інтереси суспільства лише в межах одного електорального періоду.
В. Нордхаус спробував перевірити цей висновок на підставі наявних статистичних даних для дев'яти індустріально розвинених країн (Австралія, Канада, Франція, Німеччина, Японія, Нова Зеландія, Швеція, Великобританія і США) за період 1947-1972 рр. Більш-менш задовільні результати він отримав лише щодо Франції і Швеції. Гіпотезою циклічності цього типу слід знехтувати, висловлюючись мовою статистики, для Австралії, Канади, Японії і Великобританії. Німеччина, Нова Зеландія і США виявили, на думку В. Нордхауса, помітну схожість політичного й ділового циклів. Результат порівняння теорії і практики виявився аж надто скромним. Проте праця В. Нордхауса стала піонерською і поклала початок напрямку досліджень, коли циклічність розвитку економіки намагалися пов'язати з електоральним циклом (останніми роками популярним є "політичний бюджетний цикл").
Звернемо увагу на обставину, що стосується всіх економічних моделей: вкрай спрощена, з погляду практичного економіста, ситуація потребує застосування солідного математичного апарату. Однак така доля всіх теоретичних моделей. Ми стикаємося з труднощами, намагаючись формально математично описати навіть елементарну задачу. І ці труднощі мають, мабуть, лінгвістичне походження. Відомий філософ Л. Віттгенштейн визначив їх двома тезами. По-перше, природна, тобто наша звичайна розмовна мова поліморфна, висловлювані поняття не мають чітко окреслених граней, у різних контекстах вони можуть набувати різного значення. Іншими словами, "поняття не є імена суті" — між поняттями і сутностями не має однозначного зв'язку. По-друге, "природна мова досконала" і немає потреби винаходити якусь спеціальну — кращу мову. Однак зміст праці, що багата на нові ідеї, важко передати за допомогою позначень з чіткими смисловими гранями, їх недостатньо для висловлення нових ідей. Тим часом природна мова з її нечітко окресленими поняттями набагато краще передає думку автора. У відомому сенсі слово природної мови — це певна "ложка", єдина для всіх, але її наповнення відбувається через свідомість людини і виявляється по-різному у різних людей. І тоді, оскільки кожна людина користується магазином, ринком і ощадною касою, вона може вважати себе знавцем економіки. Математична мова видається незграбною, незручною, вимагає зусиль для засвоєння. Лише одну перевагу має ця мова — вона точна, і кожне слово, кожний знак має одне лише йому притаманне значення. Проте математичні моделі стали вже природним інструментом економічної науки. Формули іноді "бачать" далі від того, що в них спочатку закладалося. У цьому — одна з причин захоплення математичними моделями. Але вони ще недосконалі і взагалі не можуть бути ефективні для розв'язання специфічних завдань сучасної ЗЕП.
Created/Updated: 25.05.2018
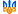 |
|