Главная Прочие дисциплины Книги Математичне програмування - Наконечний С.І.

Математичне програмування - Наконечний С.І.

2.8.2. Перехід від одного опорного плану до іншого

Розглянемо, як, виходячи з початкового опорного плану (2.40), перейти до наступного опорного плану, що відповідає цілеспрямованому процесу перебору кутових точок багатогранника розв’язків.

Оскільки 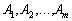є базисом m-вимірного простору, то кожен з векторів співвідношення (2.39) може бути розкладений за цими векторами базису, причому у єдиний спосіб:

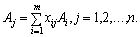
Розглянемо такий розклад для довільного небазисного вектора, наприклад, для :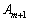

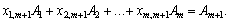(2.42)

Припустимо, що у виразі (2.42) існує хоча б один додатний коефіцієнт .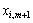

Введемо деяку поки що невідому величину 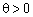, помножимо на неї обидві частини рівності (2.42) і віднімемо результат з рівності (2.41). Отримаємо:

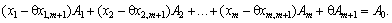(2.43)

Отже, вектор

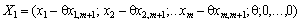
є планом задачі у тому разі, якщо його компоненти невід’ємні. За допущенням 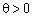, отже, ті компоненти вектора 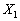, в які входять 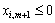, будуть невід’ємними, тому необхідно розглядати лише ті компоненти, які містять додатні 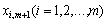. Тобто необхідно знайти таке значення 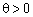, за якого для всіх 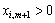буде виконуватися умова невід’ємності плану задачі:

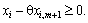(2.44)

З (2.44) отримуємо, що для шуканого 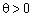має виконуватися умова 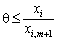. Отже, вектор 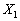буде планом задачі для будь-якого q, що задовольняє умову:

,

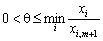де мінімум знаходимо для тих i, для яких .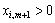

Опорний план не може містити більше ніж m додатних компонент, тому в плані 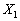необхідно перетворити в нуль хоча б одну з компонент. Допустимо, що 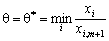для деякого значення і, тоді відповідна компонента плану 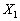перетвориться в нуль. Нехай це буде перша компонента плану, тобто:

.

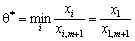Підставимо значення 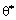у вираз (2.43):

,

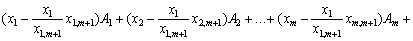
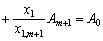якщо позначити 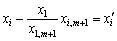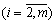, , 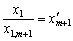то рівняння можна подати у вигляді:

,

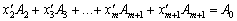якому відповідає такий опорний план:

.

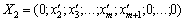Для визначення наступного опорного плану необхідно аналогічно продовжити процес: будь-який вектор, що не входить у базис, розкласти за базисними векторами, а потім визначити таке 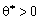, для якого один з векторів виключається з базису.

Отже, узагальнюючи розглянутий процес, можемо висновувати: визначення нових опорних планів полягає у виборі вектора, який слід ввести в базис, і вектора, який необхідно вивести з базису. Така процедура відповідає переходу від одного базису до іншого за допомогою методу Жордана—Гаусса.

Необхідно зазначити, що для випадку, коли вектор 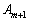підлягає включенню в базис, а в його розкладі (2.42) всі 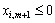, то, очевидно, не існує такого значення 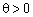, яке виключало б один з векторів. У такому разі план 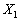містить m+1 додатних компонент, отже, система векторів 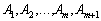буде лінійно залежною і визначає не кутову точку багатогранника розв’язків. Функціонал не може в ній набирати максимального значення. Це означає, що функціонал є необмеженим на багатограннику розв’язків.