- Цветы и растения
- Аквариум и рыбы
- Для работы
- Для сайта
- Для обучения
- Почтовые индексы Украины
- Всяко-разно
- Электронные библиотеки
- Реестры Украины
- Старинные книги о пивоварении
- Словарь старославянских слов
- Все романы Пелевина
- 50 книг для детей
- Стругацкие, сочинения в 33 томах
- Записи Леонардо да Винчи
- Биология поведения человека
Главная  Прочие дисциплины Прочие дисциплины  Книги Книги  Математичне програмування - Наконечний С.І. Математичне програмування - Наконечний С.І. |
Математичне програмування - Наконечний С.І.
3.5.1. Аналіз діапазону зміни компонент вектора обмежень
Допустимо, що деяке k-те обмеження (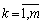 ) має в правій частині початкове значення —
) має в правій частині початкове значення — 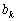 . Нехай початкова величина змінилась на величину
. Нехай початкова величина змінилась на величину 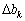 . Отже, k-те обмеження в системі (3.37) буде мати вигляд:
. Отже, k-те обмеження в системі (3.37) буде мати вигляд:
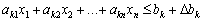 . (3.39)
. (3.39)
Для зведення (3.39) до канонічного виду необхідно ввести додаткову змінну xn+k (якщо обмеження має вигляд рівняння, то як таку змінну можна розглядати невід’ємну штучну змінну).
А. Розглянемо випадок, коли додаткова змінна в оптимальному плані небазисна і дорівнює нулю.
З першої теореми двоїстості відомо, що оптимальний план прямої задачі (як і кожен поточний опорний план) можна подати у вигляді:
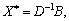 (3.40)
(3.40)
де D — матриця, що складена з компонент векторів 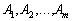 останнього базису;
останнього базису; 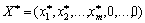 — оптимальний план задачі (3.36)—(3.38); В — вектор, що складається з вільних членів системи обмежень в останній симплексній таблиці.
— оптимальний план задачі (3.36)—(3.38); В — вектор, що складається з вільних членів системи обмежень в останній симплексній таблиці.
Отже, якщо змінюються компоненти вектора В, то змінюються також значення 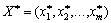 . Однак існує діапазон, у межах якого всі компоненти
. Однак існує діапазон, у межах якого всі компоненти 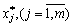 залишаються невід’ємними, тобто структура оптимального плану не змінюється. Визначимо ці межі.
залишаються невід’ємними, тобто структура оптимального плану не змінюється. Визначимо ці межі.
Вектор 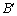 подамо у вигляді:
подамо у вигляді:
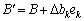 , (3.41)
, (3.41)
де ek — одиничний вектор-стовпчик, а в ньому одиниця — k-та компонента. Тоді, використовуючи (3.40), маємо:
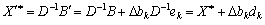 , (3.42)
, (3.42)
де dk — (добуток матриці D–1 на одиничний вектор ek) k-ий стовпчик матриці D–1.
Позначимо елементи k-го стовпчика матриці 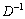 через
через 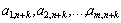 , тоді:
, тоді:
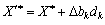 або
або 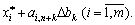
Остання симплексна таблиця буде мати вигляд:
Таблиця 3.3
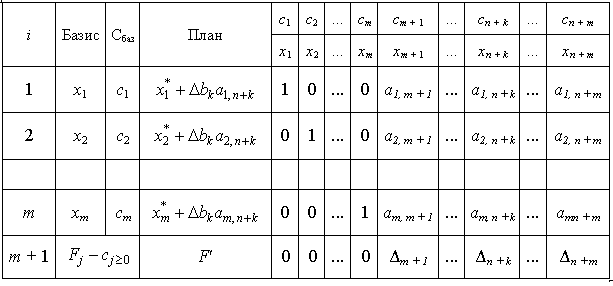
Оскільки необхідно, щоб план 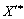 також був оптимальним, має виконуватися умова невід’ємності всіх компонент даного вектора, отже,
також був оптимальним, має виконуватися умова невід’ємності всіх компонент даного вектора, отже,
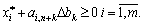 (3.43)
(3.43)
Звідси:
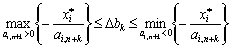 . (3.44)
. (3.44)
Тоді нижньою та верхньою границями зміни значення bk відповідно будуть:
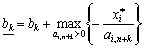 ;
;
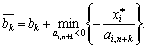
Якщо не існує жодного 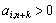 для
для  , то
, то 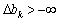 , а якщо не існує ні одного
, а якщо не існує ні одного 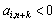 для
для 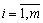 , то
, то 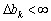 .
.
Для задачі знаходження мінімального значення цільової функції та обмежень системи типу «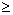 » значення Δbk змінює знак, оскільки замість нерівності
» значення Δbk змінює знак, оскільки замість нерівності 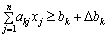 можна розглянути рівносильну нерівність
можна розглянути рівносильну нерівність 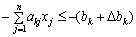 .
.
Отже, для 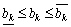 за будь-якого значення
за будь-якого значення 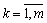 , що відповідає додатковій небазисній змінній
, що відповідає додатковій небазисній змінній 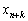 , структура оптимального плану задачі (3.36)—(3.38) залишиться постійною.
, структура оптимального плану задачі (3.36)—(3.38) залишиться постійною.
В. Розглянемо випадок, коли додаткова змінна — базисна.
Якщо додаткова змінна xn+k базисна, то це означає, що у виразі (3.42) dk –одиничний вектор з k-ою компонентою, рівною одиниці, отже, система нерівностей (3.43) перетвориться в таку:
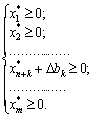
Очевидно, що значення додаткової базисної змінної визначає діапазон змін, в якому відповідна компонента bk може зменшуватись (збільшуватись для обмежень типу «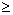 »).
»).
Оптимальний план залишається незмінним у діапазоні bk + Δbk для тих 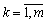 , яким відповідають додаткові базисні змінні xn + k, де
, яким відповідають додаткові базисні змінні xn + k, де
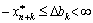 (3.45)
(3.45)
для обмежень системи (3.37) типу «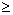 ».
».
Для задачі знаходження мінімального значення цільової функції та обмежень системи (3.37) типу «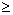 » можливі зміни компонент правої частини системи обмежень визначаються з нерівності:
» можливі зміни компонент правої частини системи обмежень визначаються з нерівності:
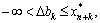 де,
де, 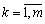 . (3.46)
. (3.46)
С. Якщо компоненти вектора вільних членів системи обмежень задачі лінійного програмування змінюються водночас для кількох чи всіх значень 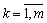 , то визначення границь можливих змін величин
, то визначення границь можливих змін величин 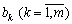 стає надто складною проблемою. Однак у такому разі завжди можна перевірити, чи задовольняють конкретні зміни величин
стає надто складною проблемою. Однак у такому разі завжди можна перевірити, чи задовольняють конкретні зміни величин 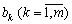 систему виду:
систему виду:
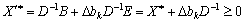 ,
,
де Е — одинична матриця. Якщо позначити елементи матриці 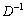 через
через 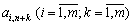 , тоді:
, тоді:
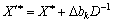 або
або 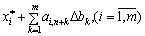 .
.
Оскільки необхідно, щоб план 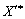 також був оптимальним, має виконуватися умова невід’ємності всіх компонент вектора, отже:
також був оптимальним, має виконуватися умова невід’ємності всіх компонент вектора, отже:
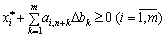 ,
,
тобто:
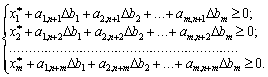 (3.47)
(3.47)
Якщо значення 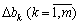 задовольняють всі нерівності системи (3.47), то структура оптимального плану задачі (3.36)—(3.38) залишається постійною.
задовольняють всі нерівності системи (3.47), то структура оптимального плану задачі (3.36)—(3.38) залишається постійною.
Для визначення верхньої та нижньої границь змін 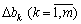 , в межах яких структура оптимального плану залишається постійною, необхідно розв’язати систему нерівностей (3.47). Однак у більшості випадків для знаходження оптимального плану нової задачі лінійного програмування
, в межах яких структура оптимального плану залишається постійною, необхідно розв’язати систему нерівностей (3.47). Однак у більшості випадків для знаходження оптимального плану нової задачі лінійного програмування 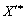 простіше розв’язати задачу симплексним методом, змінюючи вільні члени системи (3.37) на
простіше розв’язати задачу симплексним методом, змінюючи вільні члени системи (3.37) на 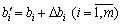 .
.
D. Для двох значень 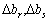 , що задовольняють систему (3.47), причому за оптимальним планом обмеження, що відповідають
, що задовольняють систему (3.47), причому за оптимальним планом обмеження, що відповідають 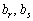 , у системі (3.37) виконуються як рівняння, можна визначити норму заміщення, що показує, наскільки необхідно збільшити (зменшити) величину
, у системі (3.37) виконуються як рівняння, можна визначити норму заміщення, що показує, наскільки необхідно збільшити (зменшити) величину 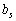 за зменшення (збільшення)
за зменшення (збільшення) 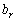 , щоб значення цільової функції залишилось незмінним.
, щоб значення цільової функції залишилось незмінним.
З третьої теореми двоїстості відомо, що за малих значень 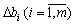 , тобто за таких значень приросту, які не змінюють значення двоїстих оцінок, а отже, задовольняють систему (3.47), виконується рівняння:
, тобто за таких значень приросту, які не змінюють значення двоїстих оцінок, а отже, задовольняють систему (3.47), виконується рівняння: 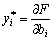 , або
, або
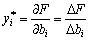 .
.
Нехай величина br змінилась на Δbr. Визначимо, як необхідно змінити bs, щоб значення цільової функції залишилось тим самим. Зміна br означає, що 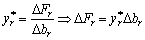 , аналогічно за зміни
, аналогічно за зміни 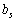 на
на 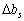 маємо:
маємо: 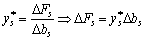 . Аби значення функціонала залишалось незмінним, необхідно, щоб
. Аби значення функціонала залишалось незмінним, необхідно, щоб
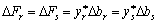 .
.
Звідси виразимо шуканий вплив 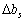 на
на 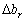 :
:
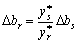 . (3.48)
. (3.48)
При відповідній заміні величин br та bs значення цільової функції задачі (3.36)—(3.38) не зміниться, проте оптимальний план буде іншим. Нехай задача (3.36)—(3.38) описує визначення оптимального плану виробництва за умов обмежених ресурсів.
Економічний зміст нерівностей (3.44), (3.45), (3.46), (3.47) полягає в тому, що вони визначають границі змін загальних обсягів ресурсів, у межах яких визначена оптимальним планом структура виробництва продукції залишається незмінною.
Рівняння (3.48) визначає, якою кількістю одного ресурсу можна замінити інший ресурс, щоб цільова функція не змінилась, причому розглядаються лише ті ресурси, які використані повністю при виробництві продукції за оптимальним планом.
Created/Updated: 25.05.2018
 |
|