Главная Прочие дисциплины Книги Математичне програмування - Наконечний С.І.

Математичне програмування - Наконечний С.І.

4.6. Аналіз коефіцієнтів матриці обмежень

Як зазначалося здебільшого коефіцієнти 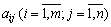матриці системи обмежень задачі лінійного програмування є технологічними коефіцієнтами (нормами витрат ресурсів на одиницю виготовлення кожного виду продукції) і не залежать від впливу випадкових чинників у такій мірі, як рівень цін чи обсяги ресурсів.

Розглянемо тільки можливі зміни тих коефіцієнтів, що відповідають небазисним змінним, оскільки зміна значень коефіцієнтів матриці обмежень, що відповідають базисним змінним, приводить до зміни базисної матриці D, і здійснити такий аналіз досить складно.

Допустимо, що за умов прикладу 4.1 додатково відомо, що витрати ресурсів на виготовлення продукції видів А та В коливаються залежно від використання різних видів устаткування в процесі виробництва продукції. За оптимальним планом виготовлення цих обох видів продукції є нерентабельним, оскільки вартість витрат ресурсів на виробництво їх одиниці продукції перевищує ціну реалізації. Проведений аналіз двоїстих оцінок, що відповідають змінним 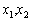, свідчить, що для виготовлення одиниці продукції виду А витрати перевищують ціну на 5 ум. од., а для виду В — у два рази менше (на 2,5 ум. од.). Отже, очевидно, що за деяких змін норм витрат ресурсів виробництво продукції виду В може стати рентабельним. З попереднього аналізу дефіцитних ресурсів відомо, що найціннішим для виробництва є третій ресурс.

Позначимо через 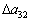величину зміни норми використання третього ресурсу на виготовлення одиниці продукції другого виду. Тоді симплексні перетворення будуть такими:

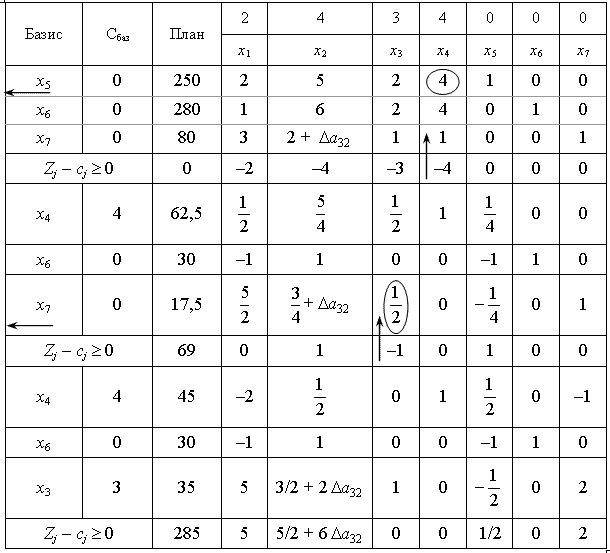
Для оптимальності плану необхідне виконання в останній симплексній таблиці умови невід’ємності всіх оцінок, тому має виконуватися нерівність:

5/2+6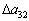 х 0,

звідки 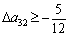. Тоді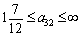

Отже, лише у разі, якщо тільки до 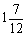ум. од. третього ресурсу буде використовуватися для виробництва одиниці продукції В, структура оптимального плану зміниться і, можливо, цей вид продукції стане рентабельним. За всіх інших змін коефіцієнта а32 в межах 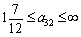структура оптимального плану буде постійною, а отже, продукція виду В буде нерентабельною.

При дослідженні зміни коефіцієнта, що відповідає базисній змінній чи одночасній зміні кількох коефіцієнтів матриці обмежень, раціональнішим буде розв’язання нової задачі лінійного програмування.