- Цветы и растения
- Аквариум и рыбы
- Для работы
- Для сайта
- Для обучения
- Почтовые индексы Украины
- Всяко-разно
- Электронные библиотеки
- Реестры Украины
- Старинные книги о пивоварении
- Словарь старославянских слов
- Все романы Пелевина
- 50 книг для детей
- Стругацкие, сочинения в 33 томах
- Записи Леонардо да Винчи
- Биология поведения человека
Главная  Прочие дисциплины Прочие дисциплины  Книги Книги  Математичне програмування - Наконечний С.І. Математичне програмування - Наконечний С.І. |
Математичне програмування - Наконечний С.І.
Заключні зауваження
Практичне застосування класичної економіко-математичної моделі транспортної задачі наштовхується на певні труднощі. Насамперед, як правило, необхідно перевозити неоднорідні продукти. Тоді транспортна задача ускладнюється. Економіко-математичну модель для багатопродуктової транспортної задачі запишемо так:
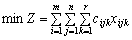
за умов: 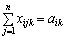 ,
,
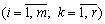 ;
;
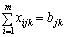 ,
,
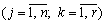 ;
;
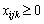 ,
,
де k — вид продукції, яку треба перевезти.
Часто господарські зв’язки між постачальниками і споживачами вимагають відповідних обмежень:
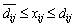 ;
;
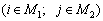 ,
,
де М1, М2 — відповідні множини індексів i, j, за якими вводяться обмеження на обсяги перевезень і-ї продукції до j-го споживача. Обмеженнями 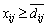 гарантується, що відповідний j-й споживач отримає і-ї продукції не менше від заданого обсягу. Обмеженнями виду
гарантується, що відповідний j-й споживач отримає і-ї продукції не менше від заданого обсягу. Обмеженнями виду 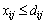 описують транспортні можливості.
описують транспортні можливості.
У класичній транспортній задачі, як правило, критерієм оптимальності є мінімізація транспортних витрат, тобто розв’язується задача на мінімум. Проте на практиці бувають випадки, коли необхідно знайти максимум цільової функції. Наприклад, необхідно розподілити робітників (верстати) між окремими видами робіт, щоб отримати максимальну сумарну продуктивність праці. Подібна ситуація має місце за оптимізації розміщення сільськогосподарських культур на ділянках землі різної якості. У такому разі критерієм оптимальності є максимізація вартості вирощеної (валової) продукції.
У класичній транспортній задачі допускається, що витрати на транспортування лінійно залежать від обсягів перевезень. Але на практиці ця умова порушується, тобто такі зв’язки, як правило, є нелінійними, стохастичними тощо. Особливої уваги заслуговує така постановка транспортної задачі, в якій необхідно мінімізувати тривалість виконання заданих обсягів робіт, наприклад, перевезення сировини та продукції, яка швидко псується. Цей критерій часто використовується для оптимізації військових операцій, виконання сільськогосподарських робіт (наприклад, збору урожаю) тощо.
Транспортна задача значно ускладнюється за моделювання виробничо-транспортних економічних систем, які виробляють продукцію в широкому асортименті, а для перевезення її застосовують різні види транспорту.
Контрольні запитання
- Опишіть економічну і математичну постановку класичної транспортної задачі.
- Чим відрізняється транспортна задача від загальної задачі лінійного програмування?
- Сформулюйте необхідну і достатню умови існування розв’язку транспортної задачі.
- Які ви знаєте властивості опорних планів транспортної задачі?
- Чим відрізняється відкрита транспортна задача від закритої?
- Як перетворити відкриту транспортну задачу на закриту?
- Які ви знаєте методи побудови опорного плану?
- Побудуйте невироджений опорний план методом північно-західного кута: для задачі:
ai = 50, 70, 90; bj = 70, 65, 70, 75.
- Що означає «виродження» опорного плану? Як його позбутися?
- Назвіть етапи алгоритму методу потенціалів.
- Як обчислюють потенціали?
- Назвіть умови оптимальності транспортної задачі.
- Опишіть економічну і математичну постановку двохетапної транспортної задачі.
- Назвіть особливості розв’язування транспортних задач з обмеженнями виду
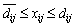 .
.
Приклади та завдання для самостійної роботи
Розв’язати наведені нижче транспортні задачі:
Задача 5.1.
| ai = (8; 10; 5); bj = (5; 5; 10); |
|
Задача 5.2.
| ai = (8; 7; 6); bj = (7; 10; 6); |
|
Задача 5.3.
| ai = (15; 10; 5; 20); bj = (10; 20; 15); |
|
Задача 5.4.
| ai = (10; 20; 40); bj = (30; 10; 60). |
|
Created/Updated: 25.05.2018
 |
|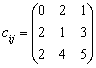 .
.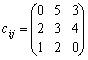 .
.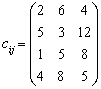 .
.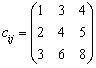 .
.