Главная Прочие дисциплины Книги Математичне програмування - Наконечний С.І.

Математичне програмування - Наконечний С.І.

8.10. Градієнтний метод

Градієнтні методи належать до наближених методів розв’язування задач нелінійного програмування і дають лише певне наближення до екстремуму, причому за збільшення обсягу обчислень можна досягти результату з наперед заданою точністю, але в цьому разі є можливість знаходити лише локальні екстремуми цільової функції. Зауважимо, що такі методи можуть бути застосовані лише до тих типів задач нелінійного програмування, де цільова функція і обмеження є диференційовними хоча б один раз. Зрозуміло, що градієнтні методи дають змогу знаходити точки глобального екстремуму тільки для задач опуклого програмування, де локальний і глобальний екстремуми збігаються.

В основі градієнтних методів лежить основна властивість градієнта диференційовної функції — визначати напрям найшвидшого зростання цієї функції. Ідея методу полягає у переході від однієї точки до іншої в напрямку градієнта з деяким наперед заданим кроком.

Розглянемо метод Франка — Вульфа, процедура якого передбачає визначення оптимального плану задачі шляхом перебору розв’язків, які є допустимими планами задачі.

Нехай необхідно відшукати

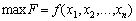
за лінійних обмежень:

;

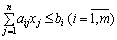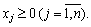
Допустимо, що Х0 — початкова точка, що належить множині допустимих планів даної задачі. В деякому околі цієї точки нелінійну цільову функцію замінюють лінійною і потім розв’язують задачу лінійного програмування. Нехай розв’язок лінійної задачі дав значення цільової функції F0, тоді з точки Х0 в напрямку F0 необхідно рухатись доти, поки не припиниться зростання цільової функції. Тобто у зазначеному напрямку вибирають наступну точку Х1, цільова функція знову замінюється на лінійну, і знову розв’язується задача лінійного програмування.

Розглянемо детальніше перехід від k-ої ітерації методу до (k + 1)-ої ітерації.

Припустимо, що відома точка Xk, яка належить області допустимих розв’язків. У даній точці обчислюємо градієнт цільової функції:

.

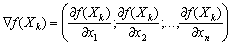Значення градієнта функції задає в даній точці напрям найшвидшого її зростання.

Замінюємо цільову функцію задачі лінійною функцією виду:

.

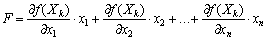Потім розв’язуємо задачу лінійного програмування з обмеженнями початкової задачі і новою цільовою функцією:

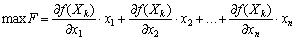
за умов:

;

.

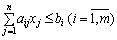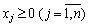Нехай розв’язком такої задачі є точка .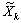

З початкової точки 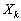в напрямку 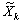рухаємося з деяким довільним кроком 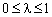, визначаючи координати нової точки 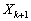у такий спосіб:

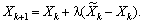
Зауважимо, що значення параметра 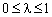доцільно вибирати таким, що дає найбільше значення цільової функції початкової задачі .

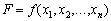Для точки Хk+1 повторюємо розглянутий процес, для чого знову розраховуємо значення градієнта і т. д.

У такий спосіб знаходимо послідовність точок 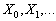, які поступово наближаються до оптимального плану початкової задачі. Ітераційний процес повторюється до того моменту, поки значення градієнта цільової функції не стане рівним нулю або виконуватиметься умова 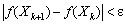, де 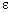— досить мале число, яке означає потрібну точність обчислень.

Підприємство виробляє два види продукції (А і В) і використовує на виробництво три види ресурсів: І, ІІ, ІІІ. Витрати ресурсів на виробництво одиниці кожного виду продукції подано в табл. 8.2.

Таблиця 8.2

Ціна реалізації одиниці продукції виду А становить 20 ум. од., проте прибуток залежить від витрат на виробництво, які пропорційні квадрату кількості виготовленої продукції. Аналогічно визначається прибуток для продукції виду В, ціна реалізації якої дорівнює 18 ум. од.

Розв’язання. Позначимо через х1 кількість продукції виду А, х2 — кількість продукції виду В, тоді загальний прибуток матиме вигляд: .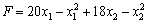

Математична модель задачі має вигляд:

,

.

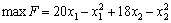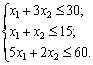
Розв’яжемо задачу методом Франка Вульфа.

І ітерація

Вибираємо точку, що належить множині допустимих планів задачі. Розглянемо, наприклад, точку .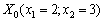

Визначимо градієнт цільової функції:

.

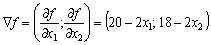В точці 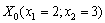обчислюємо значення градієнта:

.

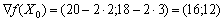Використовуючи розраховане значення градієнта, записуємо і вводимо нову цільову функцію: 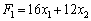. Маємо таку задачу лінійного програмування:

.

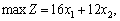
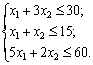
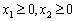Розв’язуючи цю задачу симплексним методом, знаходимо її оптимальний план: .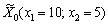

Знайдемо новий допустимий план задачі, використовуючи формулу 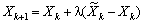для визначення координат наступної точки.

Визначаємо координати точки Х1:

, ,

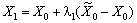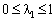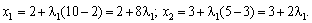
Знайдемо крок 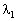такий, за якого досягається максимальне значення цільової функції. Для цього підставимо розраховані значення для х1, х2, які виражені через 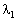, у цільову функцію :

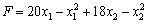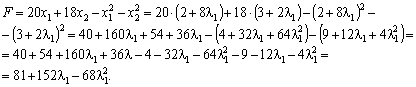
Отримали функцію, що залежить від 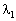. Знайдемо значення 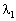, за якого функція досягає максимуму, тобто коли її похідна дорівнює нулю:

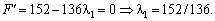Оскільки 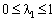, то беремо 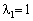. Тоді наступна точка Х1 має координати:

.

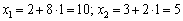Для знайденої точки 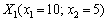обчислюємо значення цільової функції: .

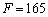ІІ ітерація

Узявши точку 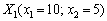, обчислюємо значення градієнта в ній:

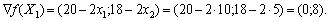
Використовуючи розраховане значення градієнта, вводимо нову цільову функцію: 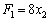. Отримуємо таку задачу лінійного програмування:

.

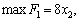
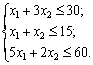
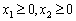Розв’язавши її симплексним методом, отримуємо оптимальний план: .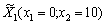

За формулою 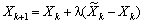визначаємо координати наступної точки наближення.

Визначаємо координати точки Х2:

,

.

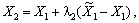
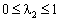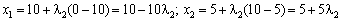Знайдемо такий крок λ2, за якого досягається максимальне значення цільової функції:

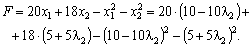
Матимемо .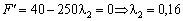

Обчислимо координати наступної точки Х2:

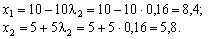
Для знайденої точки 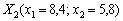значення цільової функції дорівнює: .

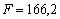Продовжуючи процес у аналогічний спосіб, на ІІІ ітерації визначаємо точку 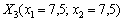і переконуємося, що значення цільової функції знову зростає: .

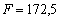На IV ітерації розраховуються координати точки 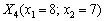, для якої .

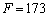V ітерація

Узявши точку 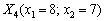, обчислюємо значення градієнта в ній:

.

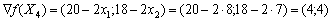Використовуючи значення цього вектора (градієнта), вводимо нову цільову функцію: 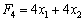і маємо таку задачу лінійного програмування:

,

.

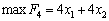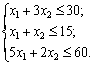
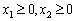Розв’язавши цю задачу, отримаємо значення оптимального плану 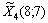, тобто повертаємося до попереднього значення. Отже, точку з координатами 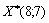вважаємо оптимальним планом, оскільки маємо нульовий градієнт функції, тобто цей план поліпшити вже не можна.