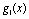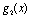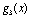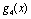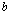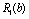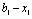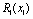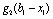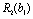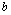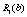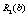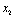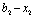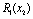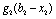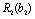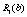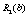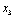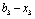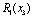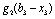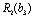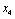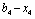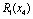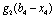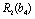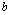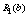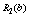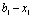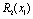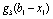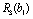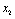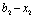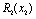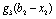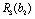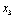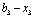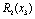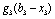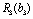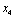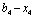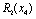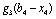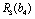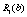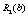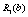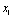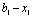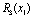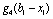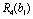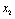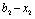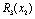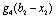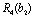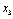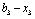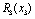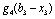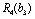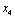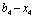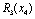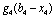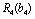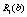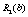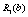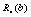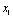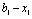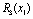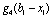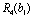- Цветы и растения
- Аквариум и рыбы
- Для работы
- Для сайта
- Для обучения
- Почтовые индексы Украины
- Всяко-разно
- Электронные библиотеки
- Реестры Украины
- Старинные книги о пивоварении
- Словарь старославянских слов
- Все романы Пелевина
- 50 книг для детей
- Стругацкие, сочинения в 33 томах
- Записи Леонардо да Винчи
- Биология поведения человека
Главная  Прочие дисциплины Прочие дисциплины  Книги Книги  Математичне програмування - Наконечний С.І. Математичне програмування - Наконечний С.І. |
Математичне програмування - Наконечний С.І.
9.3. Задача про розподіл капіталовкладень між підприємствами
Планується на наступний рік діяльність виробничої системи, яка складається з n підприємств. Відома початкова сума коштів — 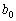 , що має бути розподілена між всіма підприємствами. Сума вкладень х приносить k-му підприємству прибуток
, що має бути розподілена між всіма підприємствами. Сума вкладень х приносить k-му підприємству прибуток 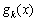 . Значення функції
. Значення функції 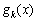
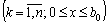 , задані таблицею.
, задані таблицею.
Необхідно визначити 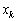 — кошти, які потрібно виділити k-му підприємству так, щоб отримати максимальний сумарний прибуток від вкладення коштів в усі підприємства
— кошти, які потрібно виділити k-му підприємству так, щоб отримати максимальний сумарний прибуток від вкладення коштів в усі підприємства 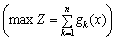 .
.
Позначимо кількість коштів, що залишилися після k-го кроку (тобто кошти, які необхідно розподілити між рештою (n – k) підприємств через 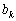 :
:
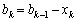
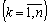 .
.
Задача розв’язується поетапно. В даному разі етапами є вкладення коштів в кожне підприємство.
І етап. Кошти вкладаються лише в одне (наприклад, перше) підприємство. Найбільший прибуток (ефективність першого етапу), що може бути отриманий, позначимо через 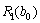 . Маємо:
. Маємо:
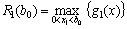 .
.
ІІ етап. Порівняємо ефективність, яку отримаємо, вкладаючи кошти лише у перше підприємство та вкладаючи кошти одночасно і в перше, і в друге підприємства. Якщо позначити ефективність другого етапу через 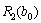 , то отримаємо:
, то отримаємо:
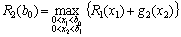 .
.
Для k-го етапу маємо рекурентне співвідношення:
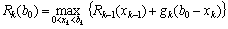 .
.
Послідовно розв’язуючи отримані рівняння, визначаємо оптимальні рішення на кожному етапі.
Наведемо найпростішу задачу динамічного програмування.
 Виробнича система складається з чотирьох філіалів. За умови здійснення реконструкції обладнання на кожному філіалі можна досягти певного приросту прибутку. Фірма виділяє на додаткові капітальні вкладення 200 тис. ум. од. (для спрощення розрахунків допустимо, що додаткові вкладення будуть здійснені в обсягах 50, 100, 150 та 200 тис. ум. од.).
Виробнича система складається з чотирьох філіалів. За умови здійснення реконструкції обладнання на кожному філіалі можна досягти певного приросту прибутку. Фірма виділяє на додаткові капітальні вкладення 200 тис. ум. од. (для спрощення розрахунків допустимо, що додаткові вкладення будуть здійснені в обсягах 50, 100, 150 та 200 тис. ум. од.).
Необхідно визначити оптимальний розподіл коштів між філіалами для максимізації загального прибутку від усіх чотирьох філіалів за умови, що відомі прирости прибутку для кожного з них (табл. 9.1):
Таблиця 9.1
Капіталовкладення, тис. ум. од. | Приріст прибутку в філіалах, тис. ум. од. | |||
1 | 2 | 3 | 4 | |
50 | 25 | 30 | 36 | 28 |
100 | 60 | 70 | 64 | 56 |
150 | 100 | 90 | 95 | 110 |
200 | 140 | 122 | 130 | 142 |
Розв’язання. В даному прикладі етапами задачі буде не час, як у попередніх викладках, а розподіл коштів між філіалами. Отже, маємо чотирьохетапну задачу динамічного програмування. Відповідно до введених раніше позначень вважатимемо, що 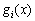 — приріст прибутку в і-му філіалі за умови капіталовкладень у нього обсягом х тис. ум. од. Умова задачі має вигляд (табл. 9.2):
— приріст прибутку в і-му філіалі за умови капіталовкладень у нього обсягом х тис. ум. од. Умова задачі має вигляд (табл. 9.2):
Таблиця 9.2
Приріст прибутку в філіалах, тис. ум. од. | |||
|
|
|
|
25 | 30 | 36 | 28 |
60 | 70 | 64 | 56 |
100 | 90 | 95 | 110 |
140 | 122 | 130 | 142 |
І етап
Найпростіший спосіб розподілу коштів, з якого починаємо розв’язування задачі, — це вкладення коштів лише у перший філіал. Якщо маємо в розпорядженні суму коштів 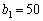 тис. ум. од., то ефективність вкладення цієї суми відповідає прибутку, що його буде отримано від інвестування в перший філіал — 25 тис. ум. од. Ефективність першого етапу позначимо через
тис. ум. од., то ефективність вкладення цієї суми відповідає прибутку, що його буде отримано від інвестування в перший філіал — 25 тис. ум. од. Ефективність першого етапу позначимо через 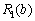 :
:
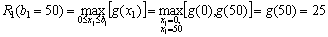 .
.
Аналогічно поступаємо у разі, коли в розпорядженні маємо суму 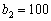 тис. ум. од. Тоді з наявних коштів вкладати можна суму величиною
тис. ум. од. Тоді з наявних коштів вкладати можна суму величиною 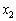 , що може набувати таких значень:
, що може набувати таких значень: 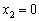 , або
, або 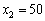 , або
, або 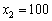 тис. ум. од. Очевидно, що з трьох названих можливих варіантів найбільшу ефективність будемо мати, вклавши кошти в сумі 100 тис. ум. од. Отже, фіксуємо найбільшу ефективність на другому кроці першого етапу —
тис. ум. од. Очевидно, що з трьох названих можливих варіантів найбільшу ефективність будемо мати, вклавши кошти в сумі 100 тис. ум. од. Отже, фіксуємо найбільшу ефективність на другому кроці першого етапу — 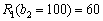 , потім на третьому кроці —
, потім на третьому кроці — 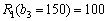 тис. ум. од. і т. д.
тис. ум. од. і т. д.
Узагальнимо всі випадки першого етапу у вигляді «таблиці найбільших ефективностей», де відображено можливі прибутки за умови різних вкладень тільки в першу філію (табл. 9.3):
Таблиця 9.3
|
|
50 | 25 |
100 | 60 |
150 | 100 |
200 | 140 |
ІІ етап
На кожному етапі необхідно зіставити ефективності прийнятих рішень на попередньому та поточному етапах. Тобто, тепер розглянемо розподіл коштів одночасно між двома філіалами фірми, порівнюючи отриманий прибуток з ефективністю попереднього етапу. Скористаємося формулою для загального випадку:
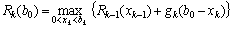 .
.
Для нашого прикладу величина 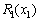 — ефективність, що дають вкладення на попередньому етапі (в даному прикладі — в перший філіал фірми), яка була розрахована на першому кроці, і позначалась через
— ефективність, що дають вкладення на попередньому етапі (в даному прикладі — в перший філіал фірми), яка була розрахована на першому кроці, і позначалась через 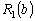 , а величина
, а величина 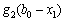 — прибуток, що дає другий філіал від залишку суми.
— прибуток, що дає другий філіал від залишку суми.
За введених у даному прикладі позначень формула набуває вигляду:
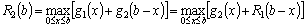
Знову спочатку допускаємо, що розподіляється сума 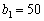 . Тоді можливі два варіанти вкладення:
. Тоді можливі два варіанти вкладення: 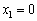 (вкладаємо кошти лише в другий філіал) або
(вкладаємо кошти лише в другий філіал) або 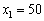 (вкладаємо кошти лише в перший філіал), тоді:
(вкладаємо кошти лише в перший філіал), тоді:
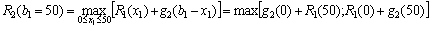
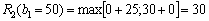 .
.
Для наочності подамо проміжні розрахунки у вигляді табл. 9.4:
Таблиця 9.4
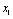 |
|
|
|
|
0 | 50 | 0 | 30 | 0 + 30 = 30 |
50 | 0 | 25 | 0 | 25 + 0 = 25 |
Стрілкою позначено найбільший з можливих прибутків за умови розподілу вкладення 50 тис. ум. од. одночасно в перший та другий філіали фірми.
У такий спосіб визначено наступний елемент «таблиці найбільших ефективностей» для випадку, коли 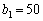 (табл. 9.5):
(табл. 9.5):
Таблиця 9.5
|
|
|
50 | 25 | 30 |
100 | 60 |
|
150 | 100 |
|
200 | 140 |
|
Потім розглядаються можливі варіанти розподілу коштів, якщо 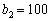 , тоді вкладати лише в другий філіал можна суму
, тоді вкладати лише в другий філіал можна суму 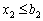 .
. 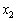 може набувати таких значень:
може набувати таких значень: 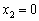 ,
, 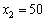 ,
, 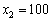 тис. ум. од. Маємо такі результати: (табл. 9.6):
тис. ум. од. Маємо такі результати: (табл. 9.6):
Таблиця 9.6
|
|
|
|
|
0 | 100 | 0 | 70 | 0 + 70 = 70 |
50 | 50 | 25 | 30 | 30 + 25 = 55 |
100 | 0 | 60 | 0 | 60 + 0 = 60 |
З табл. 9.6 висновуємо, що вкладаючи 100 тис ум. од., з усіх варіантів найбільший прибуток буде дорівнювати 70 тис. ум. од. Отже, таблиця найбільших ефективностей після цього кроку поповнюється наступним елементом (табл. 9.7):
Таблиця 9.7
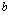 |
|
|
50 | 25 | 30 |
100 | 60 | 70 |
150 | 100 |
|
200 | 140 |
|
Аналогічно проводимо обчислення для 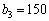 та
та 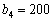 тис. ум. од.
тис. ум. од.
Нехай 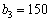 (розглядається чотири можливих варіанти розподілу, табл. 9.8):
(розглядається чотири можливих варіанти розподілу, табл. 9.8):
Таблиця 9.8
|
|
|
|
|
0 | 150 | 0 | 90 | 0 + 90 = 90 |
50 | 100 | 25 | 70 | 25 + 70 = 95 |
100 | 50 | 60 | 30 | 60 + 30 = 90 |
150 | 0 | 100 | 0 | 100 + 0 = 100 |
Нехай 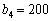 (розглядається п’ять можливих варіантів розподілу, табл. 9.9):
(розглядається п’ять можливих варіантів розподілу, табл. 9.9):
Таблиця 9.9
|
|
|
|
|
0 | 200 | 0 | 122 | 0 + 122 = 122 |
50 | 150 | 25 | 90 | 25 + 90 = 115 |
100 | 100 | 60 | 70 | 70 + 60 = 130 |
150 | 50 | 100 | 30 | 100 + 30 = 130 |
200 | 0 | 140 | 0 | 140 + 0 = 140 |
Внесемо всі розрахунки другого етапу в таблицю максимальних ефективностей, табл. 9.10:
Таблиця 9.10
|
|
|
50 | 25 | 30 |
100 | 60 | 70 |
150 | 100 | 100 |
200 | 140 | 140 |
ІІІ етап
Знову необхідно зіставити ефективності попереднього та поточного етапів. Отже, використовуємо дані, що описують прибуток, який можна отримати від вкладення одразу в перший та другий філіал (стовпчик 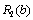 ) та прибуток від вкладення одночасно в три філіали. Знову використаємо формулу:
) та прибуток від вкладення одночасно в три філіали. Знову використаємо формулу:
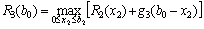
Аналогічно попереднім випадкам спочатку беремо 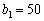 , тоді
, тоді 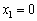 або
або 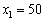 тис. ум. од., маємо (табл. 9.11):
тис. ум. од., маємо (табл. 9.11):
Таблиця 9.11
x1 |
|
|
|
|
0 | 50 | 0 | 36 | 0 + 36 = 36 |
50 | 0 | 30 | 0 | 30 + 0 = 30 |
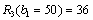 .
.
Другий крок: 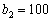 , тоді
, тоді 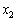 може набувати таких значень:
може набувати таких значень: 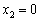 ,
, 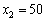 ,
, 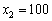 тис. ум. од. В результаті маємо (табл. 9.12):
тис. ум. од. В результаті маємо (табл. 9.12):
Таблиця 9.12
|
|
|
|
|
0 | 100 | 0 | 64 | 0 + 64 = 64 |
50 | 50 | 30 | 36 | 36 + 30 = 66 |
100 | 0 | 70 | 0 | 70 + 0 = 70 |
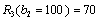 .
.
При 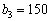 величина
величина 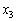 може набувати чотирьох значень:
може набувати чотирьох значень: 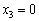 ,
, 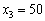 ,
, 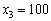 ,
, 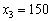 тис. ум. од., які означають частини загальної суми вкладення коштів лише в третє підприємство, відповідні їм чотири випадки:
тис. ум. од., які означають частини загальної суми вкладення коштів лише в третє підприємство, відповідні їм чотири випадки: 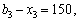
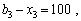
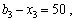
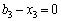 — лишки коштів, що необхідно вкладати в перші два філіали. Маємо (табл. 9.13):
— лишки коштів, що необхідно вкладати в перші два філіали. Маємо (табл. 9.13):
Таблиця 9.13
|
|
|
|
|
0 | 150 | 0 | 95 | 0 + 95 = 95 |
50 | 100 | 30 | 64 | 30 + 64 = 94 |
100 | 50 | 70 | 36 | 70 + 36 = 106 |
150 | 0 | 100 | 0 | 100 + 0 = 100 |
Отже, 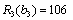 .
.
Обчислення для останнього (четвертого) кроку 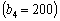 третього етапу наведені в табл. 9.14:
третього етапу наведені в табл. 9.14:
Таблиця 9.14
|
|
|
|
|
0 | 200 | 0 | 130 | 0 + 130 = 130 |
50 | 150 | 30 | 95 | 30 + 95 = 125 |
100 | 100 | 70 | 64 | 70 + 64 = 134 |
150 | 50 | 100 | 36 | 100 + 36 = 136 |
200 | 0 | 140 | 0 | 140 + 0 = 140 |
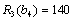 . Запишемо значення
. Запишемо значення 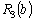 у вигляді наступного стовпчика таблиці найбільших ефективностей (табл. 9.15).
у вигляді наступного стовпчика таблиці найбільших ефективностей (табл. 9.15).
Таблиця 9.15
|
|
|
|
50 | 25 | 30 | 36 |
100 | 60 | 70 | 70 |
150 | 100 | 100 | 106 |
200 | 140 | 140 | 140 |
Аналогічно проводяться обчислення для 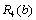 , які наводяться без коментарів.
, які наводяться без коментарів.
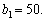
Таблиця 9.16
|
|
|
|
|
0 | 50 | 0 | 28 | 0 + 28 = 28 |
50 | 0 | 36 | 0 | 36 + 0 = 36 |
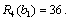
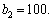
Таблиця 9.17
|
|
|
|
|
0 | 100 | 0 | 56 | 56 + 0 = 56 |
50 | 50 | 36 | 28 | 36 + 28 = 64 |
100 | 0 | 70 | 0 | 70 + 0 = 70 |
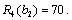
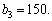
Таблиця 9.18
|
|
|
|
|
0 | 150 | 0 | 110 | 110 + 0 = 110 |
50 | 100 | 36 | 56 | 36 + 56 = 92 |
100 | 50 | 70 | 28 | 70 + 28 = 98 |
150 | 0 | 106 | 0 | 106 + 0 = 106 |
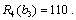
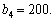
Таблиця 9.19
|
|
|
|
|
0 | 200 | 0 | 142 | 142 + 0 = 142 |
50 | 150 | 36 | 110 | 36 + 110 = 146 |
100 | 100 | 70 | 56 | 70 + 56 = 126 |
150 | 50 | 106 | 28 | 106 + 28 = 134 |
200 | 0 | 140 | 0 | 140 + 0 = 140 |
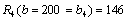 .
.
Остаточно маємо табл. 9.20:
Таблиця 9.20
|
|
|
|
|
50 | 25 | 30 | 36 | 36 |
100 | 60 | 70 | 70 | 70 |
150 | 100 | 100 | 106 | 110 |
200 | 140 | 140 | 134 | 146 |
З табл. 9.20 легко помітити, що найбільший прибуток, який дадуть всі чотири філіали за умови вкладення коштів у розмірі 200 тис. ум. од., становить 146 тис. ум. од. Повертаючись до останнього кроку розрахунків (табл. 9.19) бачимо, що число 146 відповідає змінній 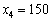 ,
, 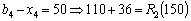 .
.
Звідси маємо, що 150 тис. ум. од. необхідно вкласти в четвертий філіал, а 50 тис. ум. од. розподілити між трьома іншими. Знову повертаємося до елементів табл. 9.20. Використання 50 тис. ум. од. на трьох перших філіалах дає загальний прибуток обсягом 36 тис. ум. од. (виділений елемент таблиці 9.20). Це значення було розраховано на ІІІ етапі, на першому кроці: 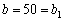 у такий спосіб (табл. 9.21):
у такий спосіб (табл. 9.21):
Таблиця 9.21
|
|
|
|
|
0 | 50 | 0 | 36 | 0 + 36 = 36 |
50 | 0 | 30 | 0 | 30 + 0 = 30 |
Отже, маємо: 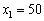 , а
, а 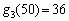 . Це означає, що 50 тис. ум. од. виділяються третьому філіалу,
. Це означає, що 50 тис. ум. од. виділяються третьому філіалу, 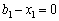 ,
, 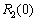 — що в перші два філіали кошти взагалі не вкладаються.
— що в перші два філіали кошти взагалі не вкладаються.
Отже, оптимальним планом задачі є: 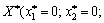

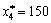 тис. ум. од.). У разі такого розподілу коштів між філіалами фірми максимальний прибуток становитиме 146 тис. ум. од.
тис. ум. од.). У разі такого розподілу коштів між філіалами фірми максимальний прибуток становитиме 146 тис. ум. од.
Created/Updated: 25.05.2018
 |
|