Главная Маркетинг Інформаційний маркетинг - Єжова Л.Ф.

Інформаційний маркетинг - Єжова Л.Ф.

3.8. Теорія масового обслуговування в задачах маркетингу

Багато економічних задач пов’язано із системами масового обслуговування (СМО), тобто такими системами, в яких, з одного боку, виникають недетерміновані масові запити (вимоги) на виконання яких-небудь послуг, а з іншого — відбувається задоволення цих запитів за певними законами. СМО включає в себе такі елементи: джерело вимог, вхідний потік вимог, черга, обслуговуючий пристрій (канал обслуговування), вихідний потік вимог. Дослідженням таких систем займається теорія масового обслуговування.

За методами теорії масового обслуговування можуть бути вирішені численні задачі в галузі маркетингу. Так, в організації торгівлі ці методи дають можливість визначити оптимальну кількість торговельних точок даного профілю, чисельність продавців, частоту завезення товарів, інші параметри. Іншим характерним прикладом систем масового обслуговування можуть слугувати склади або бази постачальницько-збутових організацій; задача теорії масового обслуговування зводиться до того, щоб установити оптимальне співвідношення між числом вимог, що надійшли на базу на обслуговування, і числом обслуговуючих пристроїв, за якого сумарні витрати на обслуговування і збитки від простою транспорту або втрати клієнтів були б мінімальними. Теорія масового обслуговування може знайти застосування і за розрахунку площі складських приміщень, при цьому складська площа розглядається як обслуговуючий пристрій, а прибуття транспортних засобів на розвантаження — як вимога.

Системи масового обслуговування (СМО) класифікуються за різними ознаками.

Залежно від умов очікування початку обслуговування вимоги розрізняють:

• СМО з втратами (відмовами);
• СМО з очікуванням (чергою).

У СМО з відмовами вимоги, що поступають у момент, коли всі канали обслуговування зайняті, дістають відмову і втрачаються. Класичним прикладом системи з відмовами є телефонна станція. Якщо абонент, що викликається, зайнятий, то вимога на з’єднання з ним дістає відмову і втрачається.

У СМО з очікуванням вимога, яка застала всі обслуговуючі канали зайнятими, ставиться у чергу аж до вивільнення будь-якого з обслуговуючих каналів.

СМО, що допускає чергу, але з обмеженим числом вимог, називаються системами з обмеженою довжиною черги.

СМО, що допускають чергу, але з обмеженим терміном перебування кожної вимоги в ній, називаються системами з обмеженим часом очікування.

За числом каналів обслуговування СМО поділяються на одноканальні та багатоканальні.

За місцем розміщення джерел вимог розрізняють СМО:

• розімкнені (коли джерела вимоги розміщені поза системою);
• замкнені (коли джерела розміщені в самій системі).

Прикладом розімкненої системи може слугувати ательє з ремонту комп’ютерів. Тут несправні комп’ютери є джерелом вимог на їх обслуговування і знаходяться поза самою системою, їх число можна вважати необмеженим.

До замкнених СМО належать, наприклад, телефонна станція, в якій устаткування є джерелом несправностей, а отже, і вимог на обслуговування їх.

Можливі й інші ознаки класифікації СМО, наприклад, за дисципліною обслуговування (обслуговується одна чи декілька вимог одночасно), однофазним і багатофазним обслуговуванням тощо.

Застосовувані в теорії масового обслуговування методи і моделі умовно поділено на аналітичні та імітаційні.

Аналітичні методи теорії масового обслуговування дають змогу отримати характеристики системи як деякі функції від параметрів функціонування її. Завдяки цьому з’являється можливість провести якісний аналіз впливу окремих факторів на ефективність роботи СМО.

Нині теоретично найбільш розроблені і зручні в практичному використанні методи рзв’язання таких задач масового обслуговування, в яких потік вимог є найпростішим (пуассонівським).

Для найпростішого потоку частота надходження вимог у систему підкоряється закону Пуассона, тобто ймовірність надходження точно k вимог за час t задається формулою

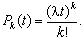• (3.10)
• Найпростіший потік характеризується трьома основними властивостями: ординарність, стаціонарність і відсутність післядії.

Ординарність потоку означає практичну неможливість одночасного надходження двох і більше вимог.

Стаціонарним називається потік, для якого математичне сподівання числа вимог, що надходять у систему в одиницю часу, не змінюється у часі. Таким чином, імовірність надходження в систему певної кількості вимог протягом заданого проміжку часу t залежить від його величини і не залежить від початку відліку його на осі часу.

Відсутність післядії означає, що число вимог, що надійшли в систему до моменту t,не визначає того, скільки вимог надійде в систему за час t + Dt.

Важливою характеристикою СМО є час обслуговування вимог у системі. Час обслуговування є, як правило, випадковою величиною, а отже, може бути описаний законом розподілу. Найбільшого поширення в теорії і особливо в практичному застосуванні набув експоненціальний закон. Функція розподілу має вигляд

F(t) = 1 – еmt. (3.11)

Імовірність того, що час обслуговування не перебільшує деякої величини t,визначаєтьсяза формулою (3.11), де m — параметр експоненціального закону часу обслуговування вимог у системі, тобто величина, обернена до середнього часу обслуговування.

Найбільш поширені на практиці СМО з очікуванням, де вимоги, що надійшли у момент, коли всі обслуговуючі канали були зайняті, стають у чергу й обслуговуються при звільненні каналів.