- Цветы и растения
- Аквариум и рыбы
- Для работы
- Для сайта
- Для обучения
- Почтовые индексы Украины
- Всяко-разно
- Электронные библиотеки
- Реестры Украины
- Старинные книги о пивоварении
- Словарь старославянских слов
- Все романы Пелевина
- 50 книг для детей
- Стругацкие, сочинения в 33 томах
- Записи Леонардо да Винчи
- Биология поведения человека
Главная  Экономика Экономика  Книги Книги  Моделювання економіки - Вітлінський В.В. Моделювання економіки - Вітлінський В.В. |
Моделювання економіки - Вітлінський В.В.
15.2. Аналіз ринку грошей
Ринок грошей — це ринок національної валюти, тобто ринок лише доларів чи лише гривень. З іншого боку, існування фінансового ринку, на котрому перебуває в обігу (як товар) низка різних інструментів — гроші, різноманітні цінні папери та їхні похідні (наприклад опціони, ф’ючерси, свопи), певні товари (наприклад золото, платина), сумнівів щодо визначення базового ринку не повинно викликати.
Тому важливо зрозуміти, що макроекономічний ринок грошей — це редукція (спрощення) фінансового (багатокомпонентного) ринку до двокомпонентного, на якому перебувають в обігу (як товар) гроші та деякий типовий представник цінних паперів (як правило, це державна облігація — коротко- чи довготермінова).
Ця модель характеризує основні макроекономічні ефекти фінансового ринку й дістала назву ринку грошей.
Найпослідовніше така редукція реалізована у концепції портфельного підходу Дж. Тобіна, котрий проілюструємо як редукцію трикомпонентного фінансового ринку до двокомпонентного. Цей підхід ґрунтується на побудові рівнянь, що описують поведінку агрегованих кредиторів і позичальників на фінансовому ринку, які формують портфель активів відповідно до своїх пріоритетів. Логіка міркування базується на тому, що n-компонентний фінансовий ринок певним чином може бути приведено (редуковано) до трикомпонентного. Далі відбувається його редукція до двокомпонентного ринку, що складається з грошей та облігацій.
Припустимо, що на макрорівні портфель агрегованого інвестора складається з трьох активів (компонент) у номінальному вираженні: грошей M, облігацій B і вартості фізичного капіталу PKK. Два останніх, не грошових, активи є або типовими представниками підмножини відносно однорідних активів, тобто активів із постійними характеристиками (дохідністю, періодом обігу, ціною тощо), або певним чином побудованих агрегатів реальних (фізичних) активів. Кожному з активів (компонент портфеля) відповідає своя норма дохідності: – p, r – p, rk, власне дефляція, реальна ставка відсотка та ефективність капіталу. Гроші розглядатимемо як актив, який приносить нульовий дохід, якщо відсутня інфляція, і від’ємний дохід у період інфляції. Щоб зберегти сенс дохідності як додатної величини, дохідність грошей вимірюється їх подорожчанням, що спостерігається у періоди дефляції.
Ставка ефективності капіталу — це вартість граничного продукту капіталу, зіставлена з одиницею вартості фізичного капіталу, тобто
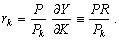
Інтегрований попит по кожному з активів подається відповідно такими функціями: L(•), J(•), N(•), які є неперервними і диференційованими за кожним аргументом функціями реального доходу Y, дохідності кожного активу і сукупного багатства A.
Отже, попит на активи у реальних цінах визначається таким чином:
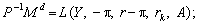
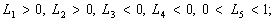
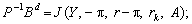
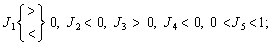
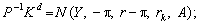
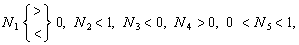
де Li, Ji, Ni, i = 1, …, 5 є відповідними частковими похідними по першому і т. д., п’ятому аргументах.
Уведені вище функції структурують попит на активи, що входять до трикомпонентного портфеля агрегованого інвестора, через знаки реакції попиту на зміну кожного з активів залежно від змін аргументів функцій попиту. Зокрема, зростання доходу збільшує попит на гроші (трансакційний попит), але не тягне за собою конкретних змін щодо попиту на капітал чи облігації. Отже, L1 > 0, а знаки похідних J1, N1 не визначені, якщо не накладати додаткових умов на відповідні функції попиту. Припускаються гіпотези, що збільшення дохідності кожного активу веде до зростання попиту на даний актив, а отже, і до скорочення попиту на альтернативні активи. Додаткова одиниця багатства розподіляється повністю на всі активи портфеля.
Попит на активи «всюди щільний», тобто мають місце рівності:
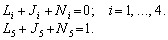
Припустимо, що облігації та фізичний капітал повністю взаємозамінні, а їхні норми дохідності рівні між собою (r – p = rk). За таких умов важко розрізнити попит окремо на кожен з них. Припустимо також, що існує однорідний попит на цінні папери [J(•) + N(•)]. Нехай державні облігації будуть репрезентативним представником такого спільного попиту на всі цінні папери. Тоді, оскільки приватне багатство визначається з умови рівноваги фінансового ринку:
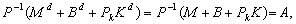
то згідно із законом Вальраса трикомпонентний фінансовий ринок можна виразити через співвідношення попиту і пропозиції грошей. Формально, звичайно, гроші та облігації є рівноправними, але, як правило, досліджується ринок грошей, оскільки пропозиція грошей — контрольована змінна, коливання якої моделює монетарну політику центрального банку.
Згідно з додатковими гіпотезами попит на гроші залежить від так званого спреду, різниці між дохідністю грошей і облігацій, тобто:
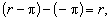
отже, попит на гроші залежить від ставки номінального відсотка r.
Таким чином, рівновагу на ринку фінансів можна подати через співвідношення між попитом на гроші в реальному вираженні:
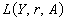
та їх пропозицією —
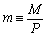 ,
,
тобто рівнянням рівноваги ринку грошей:
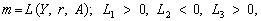 (15.6)
(15.6)
котре можна подати графічно (рис. 15.1).

Рис. 15.1. Рівновага на ринку грошей
У певному розумінні рівняння (15.6) дає інформацію про стан фінансового ринку, зведеного лише до співвідношення попиту і пропозиції грошей. Тут «ціна грошей» розуміється у кейнсіанському трактуванні, тобто як альтернативні витрати від володіння багатством у грошовій формі, чи як ставка номінального відсот- ка r. Пропозиція грошей в (15.6) — це зміна управління, хоча може бути й деякою функцією, залежною від ставки відсотка.
У проведенні монетарної політики центральний банк використовує різні інструменти регулювання облікової ставки, норми резервування, операції на вільному ринку з державними боргами тощо. Всі ці інструменти грошової політики дозволяють центральному банку управляти пропозицією грошей, хоча під його безпосереднім контролем перебуває лише так звана грошова база.
У ринковій економіці держава (центральний банк) може впливати на попит грошей лише опосередковано. Центральний банк регулює ставку відсотка, а через неї — рівень сукупного доходу, котрий є чутливим щодо ціни кредиту. Наприклад, ставка між- банківських кредитів дуже чутлива до зміни облікової ставки чи ставки рефінансування (вартості кредитів центрального банку). На рівень сукупного доходу впливає грошова маса, котра формує обсяг позичкових засобів.
Вплив монетарної політики на економіку визначається залежно від деяких апріорі заданих орієнтирів, так званих номінальних якорів, які розглянемо далі.
Зазначимо, що грошовий попит L(Y, r, A) як функція ставки відсотка (за заданих доходів і багатства) має суттєво нелінійний характер. За високих значень ставки відсотка гроші й облігації практично не є взаємозамінними. Тому грошовий попит відносно невеликий, а реакція грошового попиту на зміну ставки відсотка наближається до нуля (L2 » 0).
Можна твердити, що попит на гроші існує, практично, як трансакційний попит, що залежить лише від обсягу угод.
У цьому разі рівнянням кількості грошей буде:
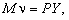
де M—величина грошового попиту; n — швидкість обігу грошей; P — дефлятор ВВП; Y — ВВП у реальному вираженні.
За малих значень ставки відсотка, навпаки, облігації і гроші (готівка) стають досить близькими субститутами, отже, попит на гроші стає досить чутливим до зміни ставки відсотка (L2 ® ?).
Цей випадок відомий у літературі як «грошова пастка» Кейнса, хоча на практиці не спостерігався.
Загалом система рівнянь (15.1) та (15.6) може бути визначеною, зокрема, для фіксованого рівня реальної пропозиції грошей 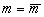 , тобто йдеться про накопичення приватного багатства у формі державних облігацій. Це дає можливість обчислити координати рівноваги реального і грошового ринків разом у результаті розв’язку системи рівнянь:
, тобто йдеться про накопичення приватного багатства у формі державних облігацій. Це дає можливість обчислити координати рівноваги реального і грошового ринків разом у результаті розв’язку системи рівнянь:
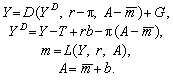 (15.7)
(15.7)
Розв’язок системи у координатах «дохід—відсоток» існує і є єдиним:
 (15.8)
(15.8)
Реакції макроекономіки на зміну параметрів системи, наприклад, ефекти стимулюючої бюджетно-податкової політики ¶G > 0, можна обчислити з розв’язку такої системи:
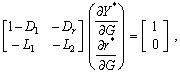 (15.9)
(15.9)
котра отримана диференціюванням рівнянь (15.7). Згідно з умовами, сформульованими для рівнянь рівноваги реального і грошового ринків, визначник системи (15.9) завжди є додатним, отже, система має єдиний нетривіальний розв’язок. Ненульовий вектор мультиплікаторів урядових витрат визначає наслідки застосування певної фіскальної політики.
Аналогічно обчислюються реакції макроекономіки на монетарну політику ¶m, а також на зміну інших параметрів системи.
Created/Updated: 25.05.2018
 |
|