- Цветы и растения
- Аквариум и рыбы
- Для работы
- Для сайта
- Для обучения
- Почтовые индексы Украины
- Всяко-разно
- Электронные библиотеки
- Реестры Украины
- Старинные книги о пивоварении
- Словарь старославянских слов
- Все романы Пелевина
- 50 книг для детей
- Стругацкие, сочинения в 33 томах
- Записи Леонардо да Винчи
- Биология поведения человека
Главная  Экономика Экономика  Книги Книги  Моделювання економіки - Вітлінський В.В. Моделювання економіки - Вітлінський В.В. |
Моделювання економіки - Вітлінський В.В.
16.2. Ставка відсотка та дисконтування
Ринкова ставка відсотка, регулюючи вартість кредиту, визначає й ринкові вимоги щодо величини дохідності капіталовкладень і попиту на них
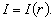
Наведемо приклад. Припустимо, що деяка компанія вирішує придбати 4 одиниці нового устаткування для його використання. Для цього вона бере позичку в 50 тис. грн для придбання кожної одиниці обладнання за ринковою ставкою 5 % щомісяця. Перша одиниця обладнання дає ефект 10 % (5 тис. грн), друга — 8, третя — 5, а четверта — 3 %, тобто 1,5 тис. грн протягом місяця. Припускаємо для спрощення, що для кредиту інтервал часу обмежено одним місяцем, його обсяг не впливає на ставку й усі витрати компанії покриваються за рахунок позички.
За умов цього прикладу для фірми є доцільним придбати лише перші три одиниці обладнання, котрі дають можливість перекрити кредит, що його взято за ринковою ставкою відсотка. Отже, ринковий відсоток — це критерій ефективності щодо здійснення інвестицій, що ілюструє рис. 16.1.

Рис. 16.1. Інвестиції та норми відсотка
Підвищення ринкової норми відсотка (ставка банківського кредиту) підвищує вимоги до інвестиційних проектів, скорочує обсяги капіталовкладень, і навпаки.
Можна стверджувати, що ринкова норма (ставка) відсотка r — це величина, яка визначає залежність поточної ціни Vt фінансового чи реального активу й дохідність його Vt+1.
Для дискретного детермінованого процесу зміни в часі вартості активу існує проста залежність між поточною вартістю активу V = Vt, отримуваним доходом Vt+1 і (постійною) ринковою чи ефективною ставкою відсотка r:
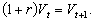 (16.1)
(16.1)
Сутність цієї формули досить проста: якщо певна сума коштів (грошей) Vt віддається в борг (інвестується в момент часу t), наприклад, на рік під r відсотків, що нараховуються одноразово, скажімо, під кінець року, то в момент (t + 1) ця сума дорівнюватиме Vt+1 гривень. Така операція інвестування має й інший еквівалентний сенс. Можна вести мову про те, що в поточний момент часу t інвестор «купує» майбутній дохід Vt+1, якщо він є відомим (його обсяг), за поточною ціною Vt гривень за умови, що альтернативні вкладення, наприклад купівля T-bills чи придбання грошового депозиту в найближчому банку, принесе йому такий самий дохід за ринковою (ефективною) ставкою відсотка r. Зазначене вище дає можливість переписати (16.1) у вигляді формули:
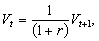
яка має сенс для відомої (очікуваної) величини майбутнього доходу. Вона встановлює зв’язок між відомим і фіксованим майбутнім доходом Vt+1, ринковою ставкою відсотка r і поточною ціною активу Vt. Згідно з цією формулою майбутній дохід дисконтується чи приводиться за допомогою ринкової ставки відсотка до величини поточної вартості активу.
Created/Updated: 25.05.2018
 |
|