| Начало раздела Производственные, любительские Радиолюбительские Авиамодельные, ракетомодельные Полезные, занимательные | Хитрости мастеру Электроника Физика Технологии Изобретения | Тайны космоса Тайны Земли Тайны Океана Хитрости Карта раздела | |
| Использование материалов сайта разрешается при условии ссылки (для сайтов - гиперссылки) | |||
Навигация: => | На главную/ Изобретения /Новые типы двигателей/ |
|
ЧУДО-КОЛЕСО ИЛИ “PERPETUUM MOBILE”?
- ОСНОВЫ ГЕОМЕТРИИ -
Смотри так же: |
Круг в геометрии является простой фигурой с известными формулами для нахождения площади и длины окружности. Формулировка звучит как фигура, у которой расстояния от центра до любой точки на окружности равны. Это расстояние обозначается радиусом "R" и является исходным для построения круга. После нахождения числа "Пи" эта фигура стала более понятной и ясной. Правильность и математическое совершенство круга привлекает, но и ограничивает его в использовании.
Предложим другую фигуру,
назовём кругом и постараемся доказать, что это круг.
Для установления родственных отношений сначала изменим само восприятие круга убрав его составляющую-радиус. И главное формулировку
этой фигуры с радиусной на диаметральную. Кругом называется фигура, у которой все прямые пересекающие ее в центре равны.
Поменяем и формулу нахождения площади с
радиусной на диаметральную. Площадь круга равна (периметр умножить на диаметр) и разделить на четыре. Слово периметр не случайно, поскольку эта формула дает площадь и другой
фигуры-квадрата. Периметр и длина окружности и сумма всех сторон квадрата. За диаметр примем и длину квадрата.
Площадь круга и квадрата можно связать и процентами. Площадь круга составляет 78,5% от площади квадрата в который вписывается
данный круг. Но основное для дальнейших
построений, это формулировка обходящаяся без радиуса.
Для создания нового круга понадобится несложный геометрический инструмент изображенный на рисунке.

Геометрический инструмент
Это прозрачный брусок, выполненный из органического стекла, в виде высокой линейки. Посередине сквозной, продольный лаз с двумя скользящими карандашами, которые легко стопорить на нужных точках. Между ними, и свободно скользящий, штырь с приспособлением позволяющим прижимать инструмент к чертежному листу. Кроме использования инструмента как линейки, его возможно использовать и как циркуль. Воспользовавшись штырем и одним карандашом (или двумя но равноудаленными от него) получим циркуль. Но основное его применение использование как «зеркало», заключается в следующем.
Возьмем одну из простых фигур — квадрат и пересечением диагоналей найдём центр установим на нём штырь и закрепим карандаши в диагональных углах. Затем, прижимая штырь, проведем одним карандашом по всему периметру квадрата и получим его отображение другим карандашом.
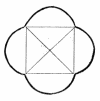
Смотри фотографию примера построения
Таким же образом используя данный инструмент, то есть взяв максимальную прямую, пересекающую фигуру в центре получим интересные результаты.
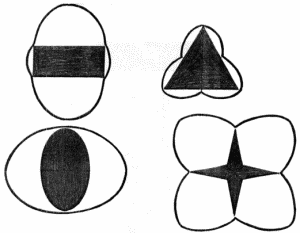
Похожими фигурами, в отличие от их математических "родственников", пользуется природа, создавая различные виды флоры и фауны.
Исходя от обратного, взяв некоторые виды организмов или растений, можно пополнить геометрический арсенал фигур. Но причём здесь механика и круг? Круг это единственная фигура не дающая отображения, или точнее сказать они полностью сообщены - круг со своим отображением. представляемая фигура тоже совмещена со своим отображением, так как является тоже кругом. Для исключения путаницы в дальнейшем, будем называть обычный круг - радиусом (или мёртвым) кругом. Математически, по единственному отличаю от такого круга, представляемую фигуру правильнее называть без радиусным кругом.
Для упрощения демонстрации его создания, возьмём за основу радиусный круг.
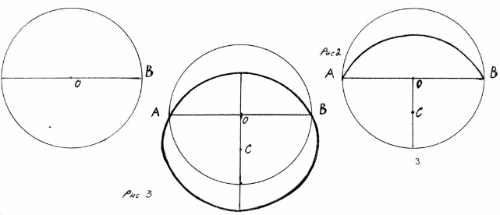
Прочертим горизонтальную прямую "АВ" пересекающую центр "О" рис.1. Из этой точки опустим перпендикуляр и выберем любую точку "С" на нём. Установив в этой (назовём её точкой отображения) точке циркуль, соединим точки А и В рис.2. Теперь воспользовавшись нашим инструментом — зеркалом, получим отображение кривой "АВ" через центр "О" замкнувшее её (рис. 3). Таким образом мы получили искомую фигуру- круг с диаметром равным кругу с которого начали работу.
Подобную фигуру можно получить
отображением трехмерного радиусного круга
на
двухмерной плоскости, прием известный всем
художникам.
Точку "С" можно выбрать и на пересечении перпендикуляра с окружностью, и можно за окружностью. Максимальное удаление от центра точки "С" это расстояние диаметра.
Из центра радиусного круга опустим перпендикуляр за окружность, возьмём циркулем расстояние "АВ" и из тачки А или В и отметим на перпендикуляре точку "С". Получим максимально возможный радиусный круг (рис.1). При увеличении расстояния круг переходит в другую фигуру (рис.2).
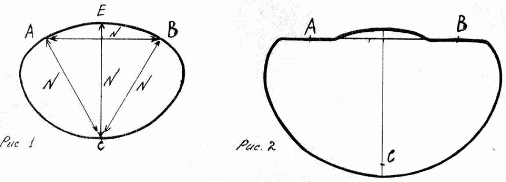
У максимального круга точка отображения "С" оказывается на окружности без радиусного круга поскольку мы взяли диаметр круга за циркульное расстояние для построения без радиусного круга (рис.1). Соединяя точки А и В циркулем из точки "С" появляется точка "Е" с расстоянием из точки "С" равное расстоянию АВ и ВС. Но радиус не может быть равным диаметру. Кроме того, прямая АВ (рис.1) делит и без радиусный круг посередине, но не по площади а по количеству точек составляющих окружность.
Парадоксально, так как вторая половина окружности ВА имеет значительно большую длину чем АВ. Оставаясь замкнутой фигурой, приходиться утверждать, что точки на половине ВА больше по длине, чем противоположные им на половине АВ.
Утверждать о равенстве площади квадрата, со стороной равной диаметру круга, с площадью без радиусного круга, и как и о равенстве длины окружности с периметром нет данных. Простая компьютерная программа для геометрических построений нахождения площадей длин окружностей и периметров не нашлась.
Будем считать доказанным существование без радиусного круга. Остановимся на этом в математических блужданиях и спорах, и практически докажем что это всё таки круг, вернее колесо способное вращаться.
Версия для печати
Автор: Elman Jamilov
P.S. Материал защищён.
Дата публикации 02.25.2004гг
Created/Updated: 25.05.2018
 |
|
