| Начало раздела Производственные, любительские Радиолюбительские Авиамодельные, ракетомодельные Полезные, занимательные | Хитрости мастеру Электроника Физика Технологии Изобретения | Тайны космоса Тайны Земли Тайны Океана Хитрости Карта раздела | |
| Использование материалов сайта разрешается при условии ссылки (для сайтов - гиперссылки) | |||
Навигация: => | На главную/Физика/ Открытия / |
|
К ВОПРОСУ ОБ ИНТЕРФЕРЕНЦИИ ВОЛН
![]()
Стецович В.И.
Рассматриваются физические процессы при образовании, распространении, интерференции и дифракции акустических волн.
Показано, что плотность энергии, которая переносится волной, пропорциональна амплитуде и частоте колебаний источника, а при интерференции волн энергия результирующего колебания равна сумме энергий складывающихся волн.
Современная волновая теория объясняет весьма обширный круг наблюдаемых в природе волновых процессов. И, тем не менее, анализ интерференционных эффектов приводит к результатам, которые противоречат выводам волновой теории.
В соответствии с общепринятыми представлениями, при сложении в некоторой точке наблюдения двух когерентных волн, распространяющихся в одном направлении:
![]()
получится вновь гармоническое колебание того же периода:
![]()
амплитуда А и начальная фаза ![]() результирующего колебания которого определяется из векторной диаграммы (рис.
1):
результирующего колебания которого определяется из векторной диаграммы (рис.
1):
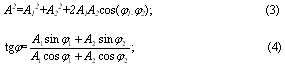
Поскольку плотность энергии волны пропорциональна квадрату амплитуды того, что колеблется, то при интерференции энергия результирующего колебания не равна сумме энергий складывающихся волн и меняется от
![]() при
при ![]() в точке интерференционного максимума до
в точке интерференционного максимума до ![]() при
при ![]() в точках интерференционного минимума.
в точках интерференционного минимума.
В простейшем случае равенства амплитуд интерферирующих волн:
![]() , амплитуда результирующего колебания меняется от нуля в минимуме до
2A в максимуме, а соответствующие интенсивности от
0 до 4A2.
, амплитуда результирующего колебания меняется от нуля в минимуме до
2A в максимуме, а соответствующие интенсивности от
0 до 4A2.
Гашение колебаний в одних местах и их усиление в других не связаны с какими-либо превращениями энергии колебаний. Таким образом, при интерференции дело сводится, как будто бы, лишь к перераспределению энергии колебаний и изменению направления ее переноса, но закон сохранения энергии строго выполняется [1].
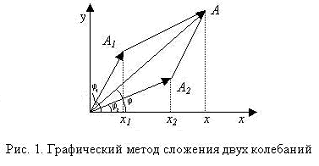
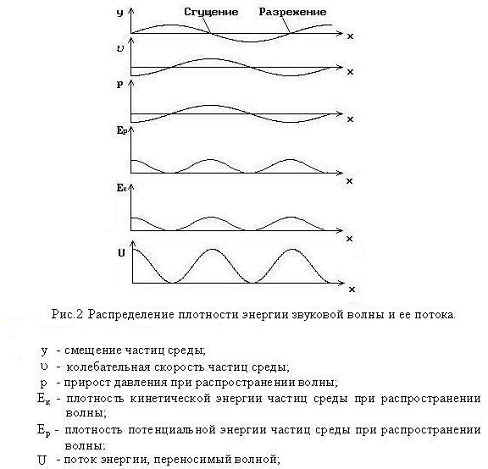
Распределение плотности энергии звуковой волны вдоль направления ее распространения, показаны на рис.2 [2]. Из рисунка видно, что, и в области сгущения и в области разрежения, волной переносятся равные потоки энергии, поэтому при интерференции двух волн, и в точке интерференционного максимума (т. А, рис.3), когда амплитуды давлений и скоростей складываются, и в точке интерференционного минимума (т. О, рис.3), когда накладывается область сгущения одной волны с областью разрежения другой, накладываются два участка волн, которые переносят одинаковую энергию, которая должна одинаково фиксироваться приборами. Тем не менее, в точках интерференционного минимума энергия не фиксируется.
Перераспределение энергии в точки интерференционного максимума возможно только в том случае если при интерференции изменяется направление переноса энергии волной. Учитывая в таком случае больший путь и постоянную скорость распространения энергии волны в среде, можно было бы зафиксировать замедление распространения энергии волны в области интерференции. Поскольку подобное не наблюдается, то следует допустить, что в области интерференции, энергия переносится волной со скоростью больше скорости распространения волны в среде, что, очевидно, нереально.
При распространении волны проходят одна через другую, совершенно не влияя друг на друга. Точно так же при прохождении точек с нулевой амплитудой колебаний при интерференции (т.
О, рис.3) две встречающиеся когерентные волны распространяются дальше без всяких изменений и в точке максимума (т.
А, рис.3) наблюдается суммирование амплитуд колебаний волн без каких-либо временных задержек. Следовательно, волны переносят энергию через точки интерференционного минимума и никакого перераспределения энергии в точки интерференционного максимума нет.
Проблемы возникают и при объяснении интерференции электромагнитных волн. Электромагнитная волна есть совокупность переменных электрического и магнитного полей, распространяющихся в пространстве и, поскольку, при наложении двух когерентных волн, в точке интерференционного минимума напряженность электрического поля равна нулю постоянно, распространение волны дальше без переменных полей (Е и
Н) через точку интерференционного минимума невозможно. Непонятно и то, в силу каких причин, после прохождения интерференционного минимума амплитуда электромагнитной волны возрастает.
При корпускулярной интерпретации явления интерференции электромагнитных волн невозможно объяснить, как в точке интерференционного максимума наблюдается выделение энергии, которое превышает сумму энергий попадающих туда фотонов, и совершенно непонятно, каким образом и куда пропадает энергия и импульс, которые переносятся фотонами, в точке интерференционного минимума и откуда они возникают после ее прохождения.
Сущность волнового процесса заключается в передаче энергии колебаний от одной точки пространства к другой и т.д. Какой же механизм передачи энергии через области пространства, где измерения показывают отсутствие волн и, соответственно, переноса энергии?
Для объяснения этих явлений представляется необходимым рассмотреть более детально процессы, проходящие при возникновении и распространении волн. Поскольку основные законы волнового движения одинаковы, будем рассматривать случай, который проще всего наглядно объяснить - распространение звуковой волны в идеальном газе.
При анализе процессов, протекающих при распространении звуковой волны в идеальном газе, будем считать, что:
- молекулы газа имеют одинаковую массу;
- при столкновениях молекул между собой - взаимодействие упругое, по законам соударения шаров;
- сталкиваются в результате движения две молекулы; одновременные столкновения трех и больше молекул маловероятны;
- частицы испытывают только лобовые столкновения, которые приводят лишь к изменению направления сталкивающихся молекул и не изменяют направления их скоростей на какие-то другие углы;
- молекулы могут двигаться в направлении координатных осей x,y,z, а из 1/3 общего количества молекул движущихся по оси х половина движется в направлении экрана, который будет источником возмущений, а другая половина от него;
Пусть под действием внешней силы экран движется со скоростью u в направлении оси х (рис.4). Произвольно выбранная молекула газа, движущаяся навстречу экрану со скоростью “-u0”, после удара будет иметь скорость u0+u. В данном случае учитывается тот факт, что температура среды и экрана одинаковы, а в процессе взаимодействия молекула сначала адсорбируется на поверхности экрана и через какое-то время вылетает, имея относительно экрана скорость u0, а относительно внешнего наблюдателя u0+u. Если рассматривать процесс взаимодействия молекулы с движущимся экраном как упругий удар шаров, то скорость молекулы будет u0+2u и все приведенные дальше формулы будут отличаться только коэффициентами.
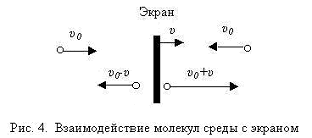
В любом случае импульс и кинетическая энергия молекул возрастают, что приводит к увеличению, по сравнению с невозмущенным состоянием, внутренней энергии газа.
С противоположной стороны экрана, после столкновения с ним, скорость молекул уменьшится: u0 -u, и внутренняя энергия газа будет меньше начального, невозмущенного состояния.
Возникшее возмущение физических параметров в среде, в результате взаимодействия между частицами по закону сохранения импульса замкнутой системы, будет распространяться со скоростью c, причем, двигаясь от экрана, половина частиц, двигающихся по оси х, переносит энергию возмущения, а после столкновения с частицами, двигающимися навстречу, в обратном направлении, энергию, соответствующую энергии частицы в невозмущенном состоянии среды (рис.5 а, б).

При движении экрана меняется и плотность частиц.
Приняв во внимание, что u«c, в области сгущения справа от экрана [3]:

В таком случае кинетическая энергия частиц в единичном объеме, переносящих энергию возмущения в направлении от экрана, равна:
![]()
а кинетическая энергия, переносимая в это же время другой половиной частиц в противоположном направлении, к экрану:
![]()
Разница между (7) и (8) определяет величину и направление переносимой волной возмущения энергии и справа от экрана, где распространяется импульс сгущения, плотность энергии волны равна:

Аналогичными вычислениями найдем плотность энергии, которая переносится волной разрежения слева от экрана:

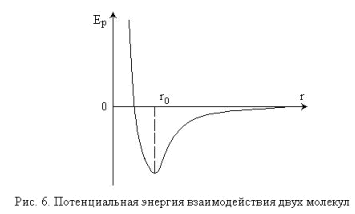
Поскольку при распространении волны меняется концентрация частиц среды, т.е. среднее расстояние между ними, значит, меняется и потенциальная энергия выделенного объема среды. В классической теории энергия волны состоит из кинетической энергии совершающих колебания частиц среды и из потенциальной энергии упругой деформации среды, причем плотности кинетической и потенциальной энергий равны в любой момент времени и в любой точке среды (рис.2).
Потенциальная энергия взаимодействия двух частиц в зависимости от расстояния между ними имеет примерно вид, показанный на
рис.6. При нормальных условиях (p=1атм, и
T=200С, r ~ 10r0), расстояние между молекулами воздуха r » rо, поэтому при распространении звуковой волны в такой среде в области разрежения потенциальная энергия среды возрастает, а в области сгущения (в отличие от классической теории) – уменьшается. Учитывая, однако, тот факт, что для молекул газа при данных условиях
Ек » Ер, изменением потенциальной энергии взаимодействия молекул, при распространении акустических волн в атмосфере, по сравнению с изменением их кинетической энергии практически можно пренебречь и газ можно рассматривать как идеальный.
Скорость колебания экрана u«c и u«u0. Тогда пренебрегая в (10) и (13) членами пропорциональными u2 и u3, довольно точно можно считать, что в общем случае, в векторной форме, плотность энергии, переносимая плоской волной:
![]()
где вектор u определяет величину энергии волны и направление ее распространения.
Если колебания экрана гармонические: х=Хsinwt и его скорость
u =Хw coswt, то значение плотности энергии, переносимой волной, принципиально отличается от значений энергии определяемых по классическим формулам
[4, с.363]: энергия волны пропорциональна плотности среды, скорости хаотического теплового движения молекул, амплитуде и частоте, а не квадратам амплитуды и частоты колебаний источника.
Составляющие энергии пропорциональные u2 и u3 вносят заметный вклад в значения энергии волны при больших амплитудах и частотах колебаний источника что, при распространении, например, акустических волн в среде, приводит к нелинейным эффектам.
Приобретенный частицами в единичном объеме среды импульс при распространении волны сгущения равен:
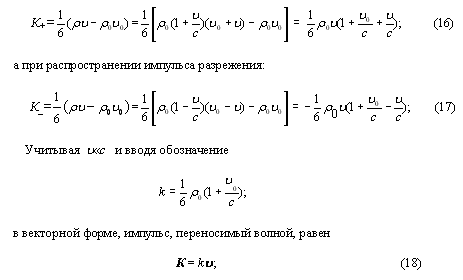
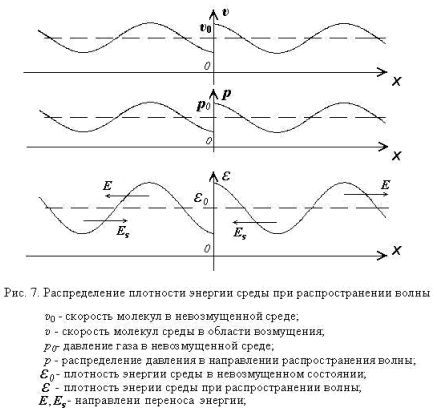
Поскольку направление скорости экрана u каждые полпериода меняется, то каждые полпериода (в отличие от классической теории) меняется и направление переносимой волной импульса и энергии. Мгновенное распределение внутренней энергии в среде и направление переноса энергии при распространении плоской волны вдоль оси х в какой-то момент времени, показаны на рис.7, где Е - направление переноса энергии волной, которая излучается источником, а Еs- направление переноса энергии за счет перераспределения внутренней энергии среды (экран размещен в начале координат). Мгновенное значение энергии переносимой волной Е(х,t) в точке х в момент времени t (рис.8) равно:
![]()
причем, положительное значения Е значит, что направление переноса энергии и распространения волны совпадают, отрицательное – энергия переносится (в отличие от классической теории) в противоположном направлении.
На практике при регистрации акустической волны и ее параметров определяют звуковое давление, а в качестве приемников акустических колебаний используют микрофоны, которые так или иначе отслеживают колебания давления среды при прохождении волны и преобразовывают их в электрические колебания, причем в классической физике интенсивность волны пропорциональна квадрату звукового давления.
Известно, что давление газа в невозмущенной среде:
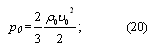
В таком случае изменение давления среды на мембрану микрофона при распространении звуковой волны, вызванное изменением плотности и скорости частиц определяется из выражения:
![]()
Замечая, что величина в скобках пропорциональна энергии, которую переносит волна, приходим к выводу, что плотность энергии волны, а, соответственно, и интенсивность звука, пропорциональна амплитуде звукового давления, а не его квадрату:
![]()
Причина всех этих отличий в том, что в классической теории при расчете энергии волны не учитывается тот факт, что частицы среды уже имеют начальную скорость и кинетическую энергию до появления возмущения в среде (рис. 7).

Принципиально отличается от общепринятого и объяснение процесса интерференции волн.
В классическом варианте, если в однородной и изотропной среде возбуждаются две когерентные волны, то в произвольной точке пространства происходит наложение волн в соответствии с принципом суперпозиции: каждая точка (молекула) среды, куда приходят две или несколько волн, одновременно принимает участие в колебаниях, вызванных каждой волной в отдельности [2]. Для определения движения частицы находят движение частицы среды в каждой волне в отдельности, а затем эти движения суммируют (рис.1).
В этом варианте: две частицы, каждая из которых переносит возмущение, вызванное двумя разными источниками колебаний, в случае взаимодействия обмениваются импульсами: первая после столкновения будет переносить до следующего столкновения импульс, переданный ей второй частицей и наоборот: вторая частица будет переносить импульс, переданный ей первой, т.е. каждая частица принимает участие в переносе возмущения только от одного источника (рис.5). Вариант взаимодействия, представленный на рис.1, возможен разве в случае одновременного удара двух частиц в третью, но, согласно начальным условиям, подобное событие маловероятно. Поэтому для частиц среды, в которой распространяются несколько волн, принцип суперпозиции неприемлем: каждая частица участвует в переносе импульса и энергии только от одного источника, или же: возмущение от разных источников переносится разными частицами.
Вследствие этого, можно утверждать: при интерференции, волны распространяются, никак не влияя одна на другую, перераспределения потоков энергии и иного взаимодействия в результате наложения волн нет, а суммарная плотность энергии в точке наблюдения равна суммарной плотности энергии интерферирующих волн:

Если две волны с одинаковыми амплитудами распространяются в одном направлении, в точках интерференционного максимума амплитуда звукового давления удваивается, а, значит, суммируются и плотности энергии складывающихся волн (рис.9а). В точках интерференционного минимума, когда накладывается область сгущения одной волны с областью разрежения другой, сигнал не фиксируется, поскольку в этом случае направления переноса энергии и импульса интерферирующими волнами противоположны, и, при равных амплитудах колебаний, их суммарное действие на мембрану микрофона равно нулю (рис.9б). Поэтому, при сложении волн, нужно учитывать не только величину энергии и импульса, переносимых волной, но и направление их переноса.
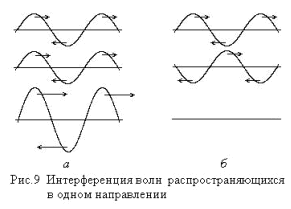
Аналогичные процессы происходят и в стоячей волне.
Известно, что когда интерферируют две когерентные, одинаковой амплитуды, бегущие в противоположных направлениях волны, результирующее волновое движение называется стоячей волной. Стоячая волна характеризуется наличием узловых точек (точки интерференционного минимума), амплитуда колебаний которых равна нулю, частицы среды в этих точках совсем не двигаются, через эти точки (согласно классическим представлениям) нет переноса энергии и, вообще, энергия не распространяется вдоль стоячей волны, только частицы между узлами колеблются и обмениваются энергией [2].
В данной интерпретации объяснение совершено иное.
В т.н. узловых точках частицы, непрерывно двигаясь, в одном направлении переносят энергию волны, бегущую в том же направлении до столкновения с частицами, которые переносят энергию волны, распространяющуюся в противоположном направлении. После столкновения и обмена импульсами в обратном направлении до следующего столкновения частицы переносят импульс волны, распространяющейся в том же направлении. Так, периодически меняя направление движения и обмениваясь импульсами, частицы поочередно переносят энергию обеих волн, поэтому они распространяются каждая в своем направлении никак не влияя друг на друга. С помощью приемников звуковых волн, например микрофона, при малых амплитудах колебаний, встречные потоки энергии и импульса через узловые точки стоячей волны и точки интерференционного минимума при интерференции волн с равными амплитудами колебаний обнаружены быть не могут, поскольку их действие на приемник одинаковое по величине, но противоположное по направлению и в результате равно нулю. Но, тем не менее, в точках интерференционного минимума волны не “гасят” друг друга, а состояние “возбуж-денных” частиц в узловых точках: скорость, энергия, а и плотность частиц, отличается от соответствующих величин в невозмущенной среде.
До сих пор, при рассмотрении вопросов распространении волн, не учитывался тот факт, что столкновения частиц приводят к изменению направлений скорости сталкивающихся частиц на какие-то углы, отличные от начального направления распространения волны. В результате этих отклонений энергия волны, переносимая частицами, может распространяться и под углом к первоначальному направлению. По площади экрана (источника волн) эти потоки энергии (в силу хаотичности процессов движения и рассеивания молекул при столкновениях) в среднем будут взаимно скомпенсированы, и лишь на боковых границах плоской волны будет наблюдаться распространение волновой энергии в сторону от первоначального направления. Аналогичные процессы будут происходить и при встрече волны с препятствием, что и является причиной дифракции волн.
Подобные процессы передачи или диффузии амплитуды колебаний вдоль волнового фронта (поперек луча) наблюдаются и при распространении волны, когда амплитуда вдоль волнового фронта меняется.
Волна переносит импульс и энергию из одного места пространства в другое, при этом считается, что все частицы среды участвующие в переносе энергии, все время колеблются около положения равновесия. Из (10),(13) и (16),(17) видно, что, при распространении продольной волны, импульс и энергия, переносимые в положительную полуволну, превышают переносимый импульс и энергию в отрицательной полуволне на величины соответственно:
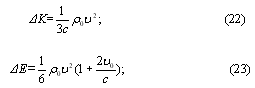
что приводит к переносу вещества среды звуковой волной, а при больших амплитудах приводит к появлению постоянного потока в виде т.н. акустических течений.
ВЫВОДЫ
-
Энергия, переносимая волной, пропорциональна амплитуде и частоте колебаний источника, а не их квадратам.
-
При интерференции энергия результирующего колебания равна сумме энергий складывающихся волн.
-
Энергия, переносимая волной возмущения, характеризуется не только величиной, но и направлением ее переноса и при распространении в среде гармонической волны, направление переноса меняется каждые полпериода.
ЛИТЕРАТУРА
-
Г.С. Ландсберг, Оптика, Наука, Москва, (1976), с. 88.
-
С.П. Стрелков, Механика, Наука, Москва, (1975), с. 481.
-
С.Е. Хайкін, Фізичні основи механіки, Радянська школа, Київ, (1966), с.674.
-
В.Е.Кузьмичев, Законы и формулы физики, Наукова думка, Киев, (1989), с. 363.
Версия для печати
Авторы: Стецович В.И.
Дата публикации 10.11.2006гг
Created/Updated: 25.05.2018
 |
|
