|
|
Начало раздела Производственные, любительские Радиолюбительские Авиамодельные, ракетомодельные Полезные, занимательные |
Хитрости мастеру Электроника Физика Технологии Изобретения |
Тайны космоса Тайны Земли Тайны Океана Хитрости Карта раздела |
|
| Использование материалов сайта разрешается при условии ссылки (для сайтов - гиперссылки) | |||
|
Навигация: => |
На главную / Физика / Исследования / |
|
БОЖЕСТВЕННЫЕ ПРОПОРЦИИ ЗОЛОТОГО СЕЧЕНИЯ
Если вы подходите к пустой скамейке и садитесь на неё, то вы сядете не посередине скамейки (как-то нескромно, хотя встречаются и такие, ярко выраженные характеры) и, конечно, не на самый край. Если вы незаметно замерите длины, на которые своим телом разделили скамейку, то обнаружите, что отношение большего отрезка к меньшему равно отношению всей длины к большему отрезку и равно примерно 1,62. Это число, называемое золотым сечением, входит в тройку самых известных иррациональных чисел, то есть таких чисел, десятичные представления которых бесконечны и непериодичны. Остальные два вы конечно знаете: это p - отношение длины окружности к диаметру и е - основание натуральных логарифмов (это слово многие не любят, но число, тем не менее, интересное). И, хотя золотое сечение и не такое фундаментальное в математике, как два друг их, оно имеет важное значение для нашего восприятия мира, так как пропорции, отвечающие золотому сечению кажутся нам гармоничными.
Золотое сечение было известно древним грекам. Вряд ли можно сомневаться в том, что некоторые древнегреческие архитекторы и скульпторы сознательно использовали его в своих творениях. Примером может служить хотя бы Парфенон. Именно это обстоятельство и имел в виду американский математик Марк Барр, когда предложил называть отношение двух отрезков, образующих золотое сечение, числом j Буква (фи) - первая буква в имени великого Фидия, который, по преданию, часто использовал золотое сечение в своих скульптурах. Одной из причин, по которой пифагорейцы избрали пентаграмму, или пятиконечную звезду, символом своего тайного ордена, является то обстоятельство, что любой отрезок в этой фигуре находится в золотом отношении к наименьшему соседнему отрезку. Многие математики, жившие в средние века и в эпоху Возрождения, были настолько увлечены исследованием необычайных свойств числа j, что это походило на легкое помешательство.
Примером могут служить слова Кеплера: «Геометрия владеет двумя сокровищами: одно из них - теорема Пифагора, другое - деление отрезка в крайнем и среднем отношении. Первое можно назвать мерой золота, втрое же больше напоминает драгоценный камень». В эпоху Возрождения отношение, выражаемое числом j, называли «божественной пропорцией» или, следуя Евклиду, «средним и крайнем отношением».
Термин «золотое сечение» вошел в употребление лишь в девятнадцатом веке. Много замечательных свойств j, проявляющихся в различных плоских и пространственных фигурах, было собрано в трактате Луки Пачоли, вышедшем в 1509 году под названием «De Divina Proportione» («О божественной пропорции») с иллюстрациями Леонардо да Винчи.
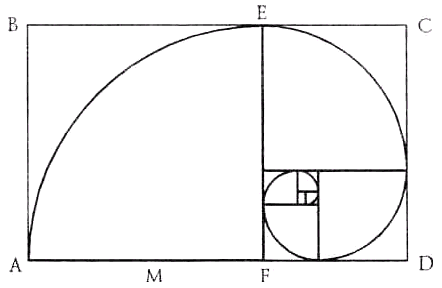
Число j выражает, например, отношение радиуса окружности к стороне правильного вписанного десятиугольника. Расположив три «золотых» прямоугольника (то есть прямоугольники, стороны которых относятся в «золотом» соотношении) так, чтобы каждый симметрично пересекался с двумя другими (под прямым углом к каждому из них), мы увидим, что вершины «золотых» прямоугольников совпадают с 12 вершинами правильного икосаэдра и в то же время указывают положение центров 12 граней правильного додекаэдра. Золотой прямоугольник обладает многими необычными свойствами. Отрезав от золотого прямоугольника квадрат, сторона которого равна меньшей стороне прямоугольника, мы снова получим золотой прямоугольник меньших размеров. Продолжая отрезать квадраты, мы будем получать все меньшие и меньшие золотые прямоугольники. Причем располагаться они будут по логарифмической спирали, имеющей важное значение в математических моделях природных объектов (например, раковинах улиток). Полюс спирали лежит на пересечении диагоналей начального прямоугольника BD и первого отрезаемого вертикального AC. Причем, диагонали всех последующих уменьшающихся золотых прямоугольников лежат на этих диагоналях.
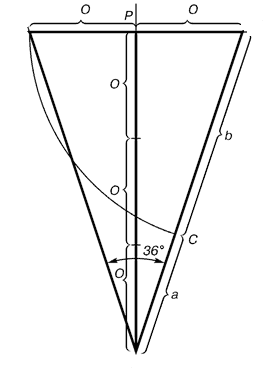
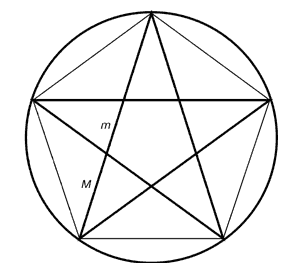
Это равнобедренный треугольник, у которого отношение длины боковой стороны к длине основания равняется 1.618. В звездчатом пятиугольнике каждая из пяти линий, составляющих эту фигуру, делит другую в отношении золотого сечения, а концы звезды являются золотыми треугольниками.
Во все времена математики, художники и философы занимались вопросами, связанными с золотым сечением. Однако вновь "открыто" и представлено ученым и художникам золотое сечение было в середине XIX в. В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд "Эстетические исследования". Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства. В своем объемистом (457 страниц) труде Адольф Цейзинг доказывает, что из всех пропорций именно золотое сечение дает наибольший художественный эффект и доставляет наибольшее удовольствие при восприятии. Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства. Именно в золотом сечении, по Цейзингу, кроется ключ к пониманию всей морфологии (в том числе строения человеческого тела), искусства, архитектуры и даже музыки. Другой немецкий ученый физиолог Густав Фехнер пытался практически обосновать взгляды Цейзинга. Для этого он измерил отношения сторон у тысяч окон, картинных рам, игральных карт, книг и других прямоугольных предметов, проверил, в каком отношении поперечные перекладины могильных крестов на кладбищах делят вертикальные основания, и обнаружил, что в большинстве случаев полученные им числа чуть отличаются от j. Фехнер разработал целый ряд остроумных тестов, в которых испытываемому предлагалось выбрать «милый его сердцу» прямоугольник из большого набора прямоугольников с различными соотношениями сторон, нарисовать самый «приятный» многоугольник, выбрать место перекладины и т.д. И здесь многократно проведенные опыты показали, что испытуемые отдают предпочтение отношениям, близким к j.
Дополнительные сведения из истории Золотого сечения можно найти на http://bullbear.msm/ru/rus/fr_main513.shtml Интересная статья Теодора Ландшейдта «Космическая функция золотого сечения», опубликованная в журнале Международного общества астрологических исследований (ISAR) «KOSMOS». В ней автор прослеживает связь таких несопоставимых явлений, как колебания солнечной оси, процент поверхности, пораженной засухой, активность питания термитов, интенсивность действия обезболивающих препаратов, индекс военной активности, вероятности рождения мальчиков - и везде колебания рассматриваемых величин находятся в отношении золотого сечения. Доктор Теодор Ландшейдт является директором Института исследований циклов солнечной активности в Канаде. Всемирно известный эксперт по вопросам солнечно-земных связей, он был отмечен премией Калифорнийского Института циклов в знак признания выдающихся достижений в этой области исследований. Особенно примечательно, что он не обошел и фрагменты фрактальных рисунков множества Мандельброта, связав увиденную там логарифмическую спираль с фрактально-хаотическими закономерностями жизни Вселенной. Ознакомиться с необычной статьей можно на http://astrologic.ru/library/golden.shtml
Желающие размяться в философских
изысканиях могут отправиться на
http://www.radiant.ru/~kbb/Page_Gold_midl.shtml
за статьей «Философское обоснование
понятия Золотая пропорция», впрочем, на наш
взгляд, не особенно глубокой.
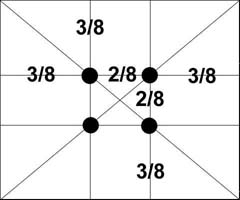
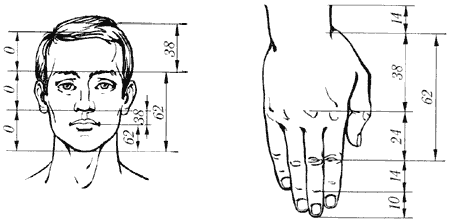
Интересный пример использования золотого сечения для получения гармоничного фотоснимка приведен на страничке, посвященной фотоискусству www.photoline.ru/tcomp1.shtml Он основан на подмеченном психологами и искусствоведами правиле - расположении основных компонентов кадра в особых точках - зрительных центрах. Таких точек всего четыре, и расположены они на расстоянии 3/8 и 5/8 от соответствующих краев плоскости. Человек всегда акцентирует свое внимание на этих точках, независимо от формата кадра или картины.
Чему же равно j? Напомним определение: большая часть относится к меньшей как все к большей. Если меньший отрезок принять за единицу, то можно записать пропорцию: ( Х+1 ) / Х = Х / 1, которая сводится к обычному квадратному уравнению Х2-Х-1=0, положительный корень которого равен . Это число одновременно выражает длину отрезка Х и значение величины j. Его десятичное разложение имеет вид 1,61803398… Если за единицу принять больший отрезок, то длина Х будет выражаться величиной, обратной j, то есть 1/j. Любопытно, что 1/j=0,61803398… Число j - единственное положительное число, которое переходит в обратное ему при вычитании единицы. Так же, это число тесно связано с метрическими свойствами некоторых правильных многоугольников и многогранников - пятиугольника, десятиугольника, додекаэдра, икосаэдра, - так как оно равно 2COS(p/5). Подобно числу p, j можно представить в виде суммы бесконечного ряда многими способами. Предельная простота следующих двух примеров еще раз подчеркивает фундаментальный характер j:j j= Число j иррациональное, не представляемое в виде простой дроби. Однако, если воспользоваться первой из приведенных формул, обрывая нашу дробь на первом, втором, третьем и т.д. знаке плюс, то получим ряд дробей, постепенно, то сверху, то снизу приближающийся к j: 1/1, 2/1, 3/2, 5/3, 8/5, 13/8, … Истинные любители математики конечно заметили, что знаменатели дробей образуют последовательность чисел, называемых числами Фибоначчи. Каждое из этих чисел, начиная со второго, равно сумме двух предыдущих. В числителе тоже находятся «предыдущие» числа Фибоначчи. Приведем один из вариантов программы, вычисляющей значение j по первому алгоритму, сложением убывающих дробей:
Dim Q As Double
Private Sub Form_Load()
Open "c:\qeqq.dat" For Output As 1
Q = 1>
For i = 1 To 24
Q = 1 + 1 / Q
Print #1, i, Q
Next i
End Sub
Программа написана на Visual Basic но этот же алгоритм можно реализовать на Паскале, Фортране, Бейсике, FoxPro - на любом доступном языке. Обратите внимание, что переменная Q объявлена как double, то есть двойной точности. Вся соль алгоритма выражена в операторе «Q=1+1/Q» который вычисляется столько раз, какой порядковый номер дроби вычисляется, все остальное служит обрамлением. Не правда ли изящно? Результатом работы программы будет таблица:
1 2
2 1,5
3 1,66666666666667
4 1,6
5 1,625
6 1,61538461538462
7 1,61904761904762
8 1,61764705882353
9 1,61818181818182
10 1,61797752808989
11 1,61805555555556
12 1,61802575107296
13 1,61803713527851
14 1,61803278688525
15 1,61803444782168
16 1,61803381340013
17 1,61803405572755
18 1,61803396316671
19 1,6180339985218
20 1,61803398501736
21 1,6180339901756
22 1,61803398820532
23 1,6180339889579
24 1,61803398867044
из которой видно, как наш
алгоритм, постепенно сужаясь, подбирается к
числу j. Аналогичным образом
можно «подбираться» к числу j
и с помощью второй формулы, через
квадратные корни:
Dim Q As Double
Private Sub Form_Load()
Open "c:\qeqq.dat" For Output As 1
Q = 1
For i = 1 To 24
Q = Sqr(1 + Q)
Print #1, i, Q
Next i
End Sub
Результат работы программы:
1 1,4142135623731
2 1,55377397403004
3 1,59805318247862
4 1,61184775412525
5 1,61612120650812
6 1,61744279852739
7 1,61785129060967
8 1,61797753093474
9 1,61801654223149
10 1,61802859747023
11 1,618032322752
12 1,61803347392815
13 1,61803382966122
14 1,61803393958879
15 1,61803397355828
16 1,61803398405543
17 1,61803398729922
18 1,61803398830161
19 1,61803398861137
20 1,61803398870709
21 1,61803398873667
22 1,61803398874581
23 1,61803398874863
24 1,6180339887495
Сравнение результатов говорит в
пользу второго метода, значения 1,618033 метод
квадратных корней достиг на двенадцатом
шагу, а метод суммирования дробей только на
шестнадцатом.
Раз уж мы так серьезно взялись за
вычисления, было бы просто нечестно
оставить без внимания трактовку золотого
сечения как отношения двух соседних членов
ряда Фибоначчи. Тем более, что сама тема
вычисления чисел Фибоначчи необычайно
интересна, так как связана с понятием
рекурсии. Что такое функция в языках
программирования все представляют (совсем
кратко - это часть программы, вызываемая для
отработки с переменным параметром). А если
функция вызывает сама себя, то такой прием
называется рекурсией. Во всех учебниках по
программированию рекурсия объясняется на
примере вычисления чисел Фибоначчи, а все
популярные статьи об этих числах
непременно упоминают рекурсию. Не
углубляясь в теоретические дебри скажем
лишь, что рекурсия позволяет писать
компактные с точки зрения объема исходного
кода программы. Но с точки зрения
оптимальности работы программы применение
рекурсии весьма сомнительно. Рассмотрим
пример (теперь на Turbo Pascal’e), вычисляющий
нужное нам золотое сечение с помощью
рекурсии. Вся изюминка в определении
функции FIB: для первого и второго значения
параметра она равна единице, а для каждого
последующего выдает сумму двух последних
значений, причем определяет их, вызывая
сама себя!
program m; uses crt;
VAR I : INTEGER ; C: CHAR ; F: TEXT;
FUNCTION FIB (T:INTEGER): LONGINT ;
begin
IF (T=1) OR (T=2) THEN
Fib:=1
ELSE Fib:=FIB(T-1)+FIB(T-2)
end;
BEGIN
ASSIGN(F,'C:\QQQ.DAT');
REWRITE(F);
CLRSCR ;
FOR I:=1 TO 24 DO BEGIN
WRITELN(F,I,' ',FIB(I),' ',FIB(i+1),' ',FIB(I+1)/FIB(I)) ;
END;
CLOSE(F);
C:=READKEY ;
END.
Рассматривая результат работы программы мы видим, как отношение двух соседних чисел Фибоначчи постепенно, то сверху, то снизу, приближается к золотому сечению.
1 1 1 1.0000000000E+00
2 1 2 2.0000000000E+00
3 2 3 1.5000000000E+00
4 3 5 1.6666666667E+00
5 5 8 1.6000000000E+00
6 8 13 1.6250000000E+00
7 13 21 1.6153846154E+00
8 21 34 1.6190476190E+00
9 34 55 1.6176470588E+00
10 55 89 1.6181818182E+00
11 89 144 1.6179775281E+00
12 144 233 1.6180555556E+00
13 233 377 1.6180257511E+00
14 377 610 1.6180371353E+00
15 610 987 1.6180327869E+00
16 987 1597 1.6180344478E+00
17 1597 2584 1.6180338134E+00
18 2584 4181 1.6180340557E+00
19 4181 6765 1.6180339632E+00
20 6765 10946 1.6180339985E+00
21 10946 17711 1.6180339850E+00
22 17711 28657 1.6180339902E+00
23 28657 46368 1.6180339882E+00
24 46368 75025 1.6180339890E+00
Значение 1,618033 появилось только
на 17 шаге, что «слабее» первых способов, но,
зато, мы получили значения 24-х членов ряда
Фибоначчи и познакомились с рекурсией. Но
программа работает не оптимально -
двадцатое значение считалось около пяти
секунд (на РIII-700, а сороковое более минуты).
Слишком много «движений» совершает
рекурсивная функция, количество их
лавинообразно растет с ростом числа,
изящность кодирования пошла во вред
производительности. А как же надо было
составлять программу для эффективной
работы? Задать массив и заполнять его такой
же функцией, но без рекурсии, обращаясь к
уже посчитанным членам ряда, помещенным в
массив. Программа будет работать «мгновенно»,
но все это будет уже не так красиво.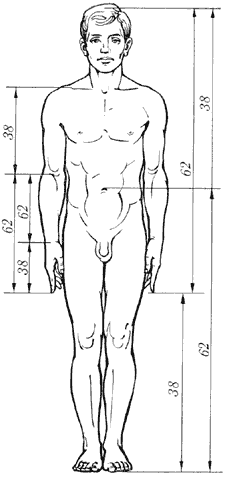
В настоящее время числа Фибоначчи усиленно изучаются бизнесменами и экономистами. Замечено, что волны, описывающие колебания котировок ценных бумаг, являются огибающими маленьких волн, те, в свою очередь, еще более мелких, а количество мелких колебаний в периоде более крупного соответствует ряду Фибоначчи. Впервые это предложил Эллиотт. Ральф Hельсон Эллиотт был инженером. После серьезной болезни в начале 1930х гг. он занялся анализом биржевых цен, особенно индекса Доу-Джонса. После ряда весьма успешных предсказаний Эллиотт опубликовал в 1939 году серию статей в журнале Financial World Magazine. В них впервые была представлена его точка зрения, что движения индекса Доу-Джонса подчиняются определенным ритмам. Согласно Эллиотту, все эти движения следуют тому же закону, что и приливы - за приливом следует отлив, за действием (акцией) следует противодействие (реакция). Эта схема не зависит от времени, поскольку структура рынка, взятого как единое целое, остается неизменной. Он писал: "Любoй человеческой деятельности присущи три отличительных особенности: форма, время и отношение, - и все они подчиняются суммационной последовательности Фибоначчи". Если вы разберетесь с числами Фибоначчи и волнами Эллиота, то можете разбогатеть, играя на бирже ценных бумаг. Заинтересовавшиеся могут зайти на сайт компании Elliott Wave International в интернете http://www.elliottwave.com/ Если плохо с английским, а разбогатеть хочется - то заходите на http://user.cityline.ru/~esfinkro/index.shtml , там есть доступно изложенная статья о Волнах Эллиота.
Интерес к золотому сечению подогревается и периодическими всплесками популярности пирамид. Например, на www.rcom.ru/tvv/Dm/str6.shtml можно найти, среди прочих знамений пирамиды Хеопса, и содержащееся в ее пропорциях золотое сечение. Не обходится и без курьезов. На упоминаемой уже странице http://bullbear.msm/ru/rus/fr_main513.shtml находим: «Длина грани пирамиды в Гизе равна 783.3 фута (238.7 м), высота пирамиды - 484.4 фута (147.6 м). Длина грани, деленная на высоту, приводит к соотношению Ф=1.618. Высота 484.4 фута соответствует 5813 дюймам (5-8-13) - это числа из последовательности Фибоначчи.» Весь юмор в том, что древние египтяне вряд ли измеряли что-либо в дюймах (вот метры - другое дело j), и появление здесь чисел Фибоначчи объяснить без мистики ну никак невозможно. Интересующимся современным пирамидостроением и необычными явлениями, происходящими в пирамидах, рекомендую статью энтузиаста пирамид Александра Голода «Пирамиды в пропорциях Золотого Сечения - генератор жизни», расположенную на http://www.slavaiv.narod.ru/ . Самая большая Пирамида высотой 44 метра построена в конце 1999 года недалеко от Москвы на 38 км шоссе Москва-Рига, ее не раз показывали по ТВ, рассказывали о происходящих в ней чудесах. Можно и не говорить, что пропорции пирамиды подчиняются рассмотренным нами соотношениям. Ну вот и все. Теперь вы не только интуитивно выберите пропорции строящегося вами дворца, но и уточните их, доведя до золотого сечения. Задание на дом. Мартин Гарднер, ведущий рубрики занимательной математики в журнале Scientific American, получил письмо от своих читателей с сообщением, что в среднем отношение роста человека к высоте пупка равно j. Надо бы это проверить, причем, женщины могут замеряться на каблуках. И для самых-самых утонченных любителей - как изменятся результаты работы трех приведенных программ, если вычисления начинать не с единицы, а, например, со ста?
Версия для печати
P.S. Материал защищён.
Дата публикации 07.03.2004гг
Created/Updated: 25.05.2018