- Цветы и растения
- Аквариум и рыбы
- Для работы
- Для сайта
- Для обучения
- Почтовые индексы Украины
- Всяко-разно
- Электронные библиотеки
- Реестры Украины
- Старинные книги о пивоварении
- Словарь старославянских слов
- Все романы Пелевина
- 50 книг для детей
- Стругацкие, сочинения в 33 томах
- Записи Леонардо да Винчи
- Биология поведения человека
Главная  Экономика Экономика  Книги Книги  Моделювання економіки - Вітлінський В.В. Моделювання економіки - Вітлінський В.В. |
Моделювання економіки - Вітлінський В.В.
5.5.2. Багатофакторні виробничі функції
В економіко-математичному моделюванні широко використовують багатофакторні виробничі функції.
Один із найбільш раціональних способів переходу від двофакторних до багатофакторних функцій полягає в такому.
Розгляньмо двофакторну функцію:
y = j1 (x1, x2). (5.8)
Аргумент x2 цієї функції розглянемо як узагальнений показник, що залежить також від двох інших чинників x3, x4:
x2 = j2(x3, x4),
де j2 — деяка функція. Підставляючи цей вираз у формулу (5.8), отримаємо трифакторну функцію
y = j1(x1, j2(x3, x4)),
що виражає залежність показника 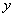 від аргументів x1, x3, x4. Цей процес можна продовжити, вважаючи, зокрема, що х3, у свою чергу, залежить від деяких чинників.
від аргументів x1, x3, x4. Цей процес можна продовжити, вважаючи, зокрема, що х3, у свою чергу, залежить від деяких чинників.
У загальному вигляді: якщо задано (п – 1) двофакторних функцій j1(x1, x2), j2(x3, x4), jn–1(x2n–3, x2n–2), то дістанемо п-факторну функцію:
y = f(x1, ..., xn)
у результаті послідовної підстановки їх. Операція такої підстановки (суперпозиції) має очевидний економічний сенс: другий аргумент, наприклад двофакторної функції, послідовно подається у вигляді залежності від показників нижчих (деталізованих) рівнів. Неважко перевірити такі властивості операції суперпозиції:
а) якщо j1, …, jn–1 — неспадні функції, то f — також неспадна функція;
б) якщо j2, …, jn–1 — лінійно-однорідні функції, а j1 — однорідна функція ступеня однорідності g, то f — однорідна функція ступеня однорідності g;
в) якщо j1, …, jn — увігнуті неспадні функції, то f — увігнута неспадна функція.
Отже, якщо двофакторні функції j1, …, jn–1 є неокласичними, то отримана в результаті їх суперпозиції функція f також буде неокласичною.
Для виробничих функцій від n змінних справедливими є твердження, які показують, що клас функцій, поданих у вигляді суперпозиції будь-яких двофакторних функцій, є досить широким. Строго доводиться, зокрема, що будь-яка неперервна функція f(x1, …, xn) від n змінних (за умови n ? 4) може бути подана у вигляді суперпозиції неперервних функцій від трьох змінних. У свою чергу кожна неперервна функція від трьох змінних може бути отримана як суперпозиція функцій від двох змінних. Відомо також, що будь-яку неперервну функцію від двох змінних можна з будь-якою заданою точністю апроксимувати суперпозицією неперервних функцій від однієї змінної та функції y = x1 + x2.
Перелік та окремі характеристики деяких класів багатофакторних виробничих функцій наводяться у низці підручників*2.
*2: {Клейнер Г. Б. Производственные функции: Теория, методы, применение. — М.: Финансы и статистика, 1986.}
Created/Updated: 25.05.2018
 |
|