Главная Экономика Книги Моделювання економіки - Вітлінський В.В.

Моделювання економіки - Вітлінський В.В.

5.6. Макроекономічні виробничі функції

Як зазначалося у попередньому матеріалі, виробнича функція (ВФ) відображає залежність результату від витрат ресурсів. У формалізованому описі економіки (точніше, її виробничої підсистеми) за допомогою ВФ ця підсистема розглядається як «чорна скринька», на вхід якої постачають ресурси R1, …, Rn, а на виході отримують результати у вигляді річних обсягів виробництва різних видів продукції X1, …, Xm.

Як ресурси (чинники виробництва) на макрорівні здебільшого розглядаються накопичена (уречевлена) праця у формі виробничих фондів (капітал) K і поточна (жива) праця L. А як результат — валовий випуск X (чи валовий внутрішній продукт Y, чи національний дохід N). У всіх випадках результат узагальнено називатимемо випуском і позначатимемо через X.

Стосовно до обґрунтування чинника K можна твердити, що минула праця втілена в основних і обігових, виробничих і невиробничих фондах.

Вибір конкретної структури K визначається метою дослідження, а також структурою розвитку виробничої і невиробничої сфер упродовж досліджуваного періоду часу. Якщо в цей період у невиробничу сферу вкладається приблизно постійна частка ново- створеної вартості, і невиробнича сфера має приблизно однаковий вплив на виробництво, то це є підставою для того, щоб у ВФ враховувати лише виробничі фонди. Виробничі фонди складаються з основних і обігових. Якщо структура їх (співвідношення між цими складовими) приблизно постійна впродовж періоду, за який вивчається об’єкт дослідження, то достатньо враховувати у ВФ лише основні виробничі фонди.

Отже, економіка заміщується своєю моделлю у формі, взагалі кажучи, нелінійної ВФ:

X = F(K, L), (5.9)

тобто випуск продукції є функцією від затрат ресурсів (фондів і праці).

Далі аналізуватимемо основні характеристики ВФ на прикладі неокласичної мультиплікативної ВФ (зокрема функції Кобба—Дугласа) та деяких інших, що використовуються в економічних моделях на макроекономічному рівні.

Виробничу функцію X = F(K, L) називають неокласичною, якщо вона є гладкою і задовольняє умови, які мають чітку, несуперечливу, обґрунтовану економічну інтерпретацію:

1) F(0, L) = F(K, 0) = 0 — за відсутності одного з ресурсів виробництво не є можливим;

2) 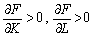 — зі зростанням обсягів ресурсів зростає й випуск;

3) 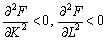 — зі зростанням обсягів ресурсів швидкість зростання випуску знижується;

4) F(+?, L) = F(K, +?) = ? — за необмеженого зростання обсягів одного з ресурсів випуск також необмежено зростає.

Мультиплікативна ВФ задається виразом:

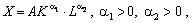(5.10)

де А — коефіцієнт нейтрального технічного прогресу; ?1, ?2 — коефіцієнти еластичності за фондами K і працею L відповідно. Отже, ВФ (5.10) має властивість 1, що є адекватним реальній економіці: за відсутності одного з ресурсів виробництво неможливе.

Частковим випадком неокласичної мультиплікативної ВФ є функція Кобба—Дугласа:

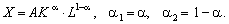
Мультиплікативна ВФ визначається за даними часового ряду випуску і витрат ресурсів (Xt, Kt, Lt), t = 1, …, T, де Т — довжина часового ряду, і вважається, що має місце Т співвідношень:

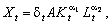
де dt — коригуючий випадковий коефіцієнт, який приводить у відповідність фактичний і теоретичний випуски і відображає флуктуацію результатів під впливом низки інших (випадкових) чинників, окрім цього, математичне сподівання Md = md = 1.

Оскільки в логарифмах ця функція є лінійною:

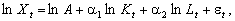
де et = lndt, Me = me = 0, то отримуємо модель лінійної множинної регресії. Параметри функції: А, a1, a2 можуть бути визначені з використанням методу найменших квадратів за допомогою низки стандартних пакетів прикладних програм, які реалізують метод множинної регресії (приміром, STATGRAF чи SAS для персональних ЕОМ).

Як приклад можна навести мультиплікативну функцію валового випуску продукції однієї з країн, яка обчислюється на підставі статистичних даних за декілька років і систематично оновлюється на основі використання нових даних за поточний період. Зокрема, виходячи з даних за 1960—1994 рр. можна подати виробничу функцію (валовий випуск) Російської Федерації (млрд руб.) залежно від вартості основних виробничих фондів (млрд руб.) і чисельності зайнятих у народному господарстві (млн осіб) (усі вартісні показники наведено у порівнянних цінах для даного періоду):

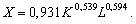(5.11)

Мультиплікативна функція задовольняє також властивість 2, що є адекватним реальній економіці: зі зростанням витрат ресурсів випуск також зростає, тобто:

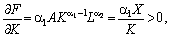оскільки 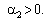(5.12)

Частинні похідні випуску за чинниками, що їх називають граничними продуктами, або граничними (маржинальними) ефективностями чинників, є приростом випуску на малу частку приросту чинника:

— граничний продукт фондів (гранична фондовіддача, гранична ефективність фондів);

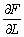— граничний продукт праці (гранична продуктивність праці, гранична ефективність праці).

Для мультиплікативної функції з (5.12) випливає, що гранична фондовіддача пропорційна середній фондовіддачі 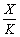з коефіці- єнтом a1, а гранична продуктивність праці — середній продуктивності праці 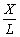з коефіцієнтом пропорційності a2:

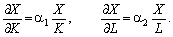(5.13)

Із рівнянь (5.13) випливає, що за a1 < 1, a2 < 1 граничні віддачі чинників є меншими від середніх; за цих умов мультиплікативна функція має властивість 3, що часто спостерігається у реальній економіці: зі зростанням витрат ресурсу його гранична віддача спадає, тобто:

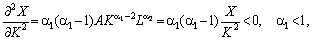
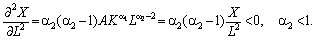(5.14)

Із (5.10) також зрозуміло, що мультиплікативна функція має властивість 4, тобто за необмеженого зростання обсягу одного з ресурсів випуск також необмежено зростає. Таким чином, мультиплікативна функція 0 < a1 < 1, 0 < a2 < 1 є неокласичною.

Здійснимо економічну інтерпретацію параметрів А, ?1, ?2 мультиплікативної ВФ.

Параметр А здебільшого інтерпретують як параметр нейтрального технічного прогресу: за тих самих значень ?1 і ?2 випуск у точці (K, L) буде тим більшим, чим більше А.

Для інтерпретації параметрів ?1 і ?2 скористаємось поняттям коефіцієнтів еластичності. Існує поняття еластичностей як логарифмічних виробничих чинників:

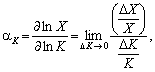(5.15)

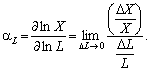
Оскільки у нашому випадку

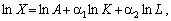
то

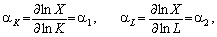
тобто ?1 — коефіцієнт еластичності випуску за основними фондами, а ?2 — коефіцієнт еластичності випуску за працею.

Із (5.15) видно, що коефіцієнт еластичності чинника показує, на скільки відсотків збільшиться випуск, якщо чинник зросте на 1 %.

Наприклад, згідно з ВФ (5.11) збільшення основних фондів (ОФ) на 1 % приведе до зростання валового випуску на 0,539 %, а збільшення зайнятих на 1 % — на 0,594 %. Якщо ?1 > ?2, то має місце працеощадне (інтенсивне) зростання.

Розгляньмо темпи зростання випуску:

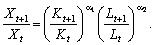(5.16)

Якщо піднести обидві частини (5.16) до степеня 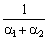, то отримаємо співвідношення

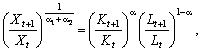(5.17)

у якому праворуч — зважене середньогеометричне темпів зростання витрат ресурсів, де ваговими коефіцієнтами слугують відносні коефіцієнти еластичності чинників:

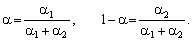
Якщо ?1 + ?2 > 1, то випуск зростає швидше, ніж у середньому зростають чинники, а якщо ?1 + ?2 < 1 — повільніше. Справді, якщо чинники (їх обсяги) зростають, тобто Kt+1 > Kt, Lt+1 > Lt, то згідно з (5.16) зростає і випуск (тобто Xt+1 > Xt), отже, за ?1 + ?2 > 1:

Темпи зростання випуску є більшими ніж середні темпи зростання чинників. Отже, якщо ?1 + ?2 > 1, то ВФ описує зростаючу економіку.

Лінією рівня на площині K, L, чи ізоквантою, називають множину тих точок площини, для котрих F(K, L) = X0 = const.

Для мультиплікативної ВФ ізокванта має вигляд:

або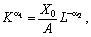

тобто це є степенева гіпербола, асимптотами якої є осі координат.

Для різних обсягів K, L, що лежать на конкретній ізокванті, випуск дорівнює значенню X0, що є еквівалентним твердженню про взаємозаміщення ресурсів. Оскільки на ізокванті F(K, L) = = X0 = const, то

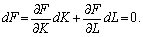(5.18)

У цьому співвідношенні 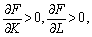тому dK і dL мусять мати різні знаки: якщо dL < 0, що означає скорочення обсягів праці, то dK > 0, тобто зменшення в обсязі 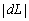, праця заміщується фондами в обсязі dK.

Слушним є таке означення, що випливає з (5.18). Граничною нормою заміщення (заміни) праці фондами SK називають відношення модулів диференціалів ОФ і праці:

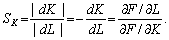
І, відповідно, гранична норма заміщення фондів працею (SL):

.

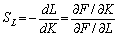Легко помітити, що SK • SL = 1.

Для мультиплікативної виробничої функції норма заміщення праці фондами пропорційна фондоозброєності:

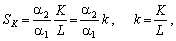
що є природним, адже брак обсягів праці можна компенсувати її кращою фондоозброєністю.

Ізокліналями називають лінії найшвидшого зростання ВФ. Ізокліналі ортогональні лініям нульового зростання, тобто ортогональні ізоквантам. Оскільки напрямок найшвидшого зростання у кожній точці (K, L) задається градієнтом

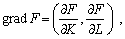
то рівняння ізокліналі можна записати таким чином:

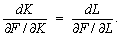
Зокрема, для мультиплікативної ВФ маємо:

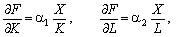
тому ізокліналь можна задати диференціальним рівнянням:

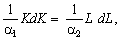
котре має розв’язок

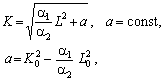
де K0, L0 — координати точки, через яку проходить ізокліналь.

Якщо припустити, що a = 0, то отримаємо рівняння ізокліналі, що проходить через відповідні точки площини (вона є прямою лінією):

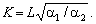
На рис. 5.1 зображені ізокванти та ізокліналі мультиплікативної ВФ.

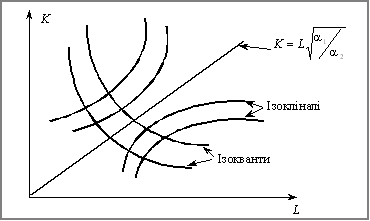
Рис. 5.1. Ізокванти та ізокліналі мультиплікативної ВФ

Аналізуючи чинники зростання економіки, виокремлюють екстенсивний чинник зростання (за рахунок збільшення обсягів витрат ресурсів, тобто збільшення масштабу виробництва) та інтенсивний чинник зростання (завдяки підвищенню ефективності використання ресурсів).

Як за допомогою ВФ вирізнити та описати масштаб та ефективність виробництва?

Це можна здійснити, якщо випуск і витрати будуть виражені у співвимірних одиницях, наприклад у вартісній формі. Найпростіше перейти до відносних (безрозмірних) показників вимірювання. У даному випадку ВФ можна подати так:

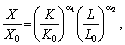(5.20)

де X0, K0, L0 — значення обсягів випуску і витрат фондів і праці в базовому році.

Безрозмірну форму (5.20) треба просто привести до початкового вигляду:

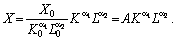
Отже, коефіцієнт A отримує економічно прозорий зміст:

,

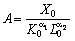який зіставляє ресурси з випуском. Якщо позначити випуск і ресурси у відносних (безрозмірних) одиницях вимірювання через 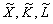, то ВФ у формі (5.20) можна подати таким виразом (через ):

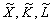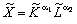, (5.21)

де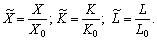

Відшукаємо тепер аналітичний вираз стосовно до ефективності економіки, скориставшись виразом (5.21).

Нагадаймо, що ефективність — це відношення результату до витрат. У нашому випадку — два види витрат: витрати минулої праці у вигляді фондів 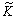і живої праці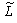. Отже, маємо два часткових показники ефективності: 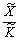— фондовіддача, 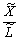— продуктивність праці.

Оскільки часткові показники мають однакову розмірність (вони безрозмірні), то можна знаходити будь-які середні з них. Оскільки ВФ виражена в мультиплікативній формі, то і середнє природно взяти у такій самій формі, тобто як зважене середньогеометричне часткових показників ефективності:

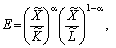(5.22)

роль вагових коефіцієнтів тут відіграють відносні еластичності:

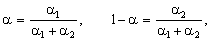
тобто часткові ефективності входять до загальної (узагальненої) ефективності з такими самими пріоритетами, з якими входять у ВФ відповідні ресурси.

Із (5.22) випливає, що за допомогою коефіцієнта економічної ефективності ВФ можна подати у формі, яка зовнішньо збігається з функцією Кобба—Дугласа:

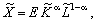(5.23)

але у співвідношенні (5.23) E — не постійний коефіцієнт, а функція від (K, L).

Оскільки масштаб виробництва М подається в обсягах витрачених ресурсів, то, враховуючи ті самі міркування, що й у випадку побудови узагальненого показника економічної ефективності, визначимо і зважене середньогеометричне використаних ресурсів (як масштаб виробництва):

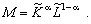(5.24)

Із (5.23) і (5.24) отримаємо, що випуск 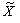є добутком економічної ефективності та масштабу виробництва:

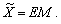(5.25)

Приклад Розгляньмо знайдену за даними 1960—1995 рр. виробничу функцію валового внутрішнього продукту США:

.

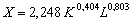Обчислимо масштаб та ефективність виробництва.

Валовий внутрішній продукт США, що вимірюється в млрд дол. у цінах 1987 р., зріс з 1960 до 1995 р. у 2,82 раза, тобто 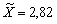; основні виробничі фонди за цей самий період збільшились у 2,88 раза (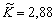), а чисельність зайнятих — у 1,93 раза ().

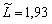Розв’язання. Обчислимо відносні еластичності за фондами і працею:

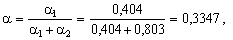1 – a = 0,6653.

Визначимо тепер часткові ефективності ресурсів:

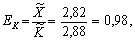
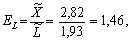
а також знайдемо узагальнений показник ефективності як зважене середньогеометричне часткових показників:

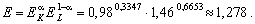
Масштаб обчислюємо як зважене середньогеометричне темпів зростання ресурсів:

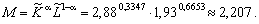
Отже, загальне зростання ВВП з 1960 до 1995 р. у 2,82 раза стало можливим завдяки зростанню масштабу виробництва у 2,307 раза і підвищенню ефективності виробництва у 1,278 раза (2,82 = 1,273 ? 2,207).

Виробничу функцію називають однорідною степеня g, якщо:

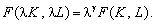(5.26)

Мультиплікативна функція є однорідною степеня a1 + a2.

Що ж до однорідних ВФ, то можна отримати спрощений вираз для норми заміщення. Дійсно,

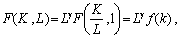
де 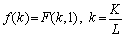— фондоозброєність. Тому

звідси маємо:

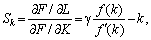(5.27)

тобто норма заміщення є функцією лише фондоозброєності.

Для однорідних ВФ уводять поняття еластичність заміни праці фондами bK:

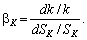(5.28)

Ця величина показує, на скільки відсотків необхідно змінити фондоозброєність, щоб досягти зміни норми заміщення на один відсоток. Аналогічно вводиться і показник еластичності заміни фондів працею bL.

Легко перевірити, що bK = bL = b.

Для мультиплікативних ВФ b = 1. Справді, у цьому випадку

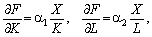
тому

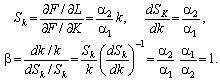
Клас ВФ з постійною еластичністю заміни (CES-функцій) будується, зокрема, таким чином:

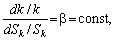
звідси маємо: 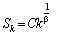(знаходиться інтегруванням). Тут С — довільна константа. Підставляючи останній вираз у (5.27), дістанемо:

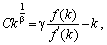або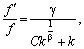

звідси

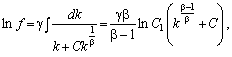
де С1 — довільна константа.

У результаті дістаємо:

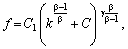
або у змінних K, L

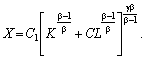
Якщо ввести позначення:

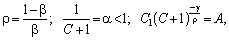
то дістанемо загальний вигляд функції з постійною еластичністю заміщення (CES-функцію).

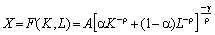. (5.29)

У цій функції A > 0, оскільки X — це випуск, а якщо 0 < g ? 1, r > –1, то вона задовольняє умови 2 і 3 для неокласичних ВФ. Якщо g = 1, b ® 1 (r ® 0), то CES-функція прямує до функції Кобба—Дугласа, а коли b ® 0 — до функції з фіксованими пропорціями X = min(Kg, Lg), котра описує випадок заміни (заміщення) чинників (b = 0). Якщо (r ® –1, g = 1, то CES-функція переходить у лінійну функцію вигляду X = EKK + ELL, де EK = Aa = =  A(1 – a).