- Цветы и растения
- Аквариум и рыбы
- Для работы
- Для сайта
- Для обучения
- Почтовые индексы Украины
- Всяко-разно
- Электронные библиотеки
- Реестры Украины
- Старинные книги о пивоварении
- Словарь старославянских слов
- Все романы Пелевина
- 50 книг для детей
- Стругацкие, сочинения в 33 томах
- Записи Леонардо да Винчи
- Биология поведения человека
Главная  Финансы Финансы  Книги Книги  Фінансова статистика - Шустіков А.А. Фінансова статистика - Шустіков А.А. |
Фінансова статистика - Шустіков А.А.
13.5. Конверсія фінансових рент
Конверсією фінансових рент називається заміна потоку рентних платежів іншим платежем. У простому вигляді зміна умов ренти полягає в заміні ренти одночасним платежем. Також кілька рент можуть бути об’єднані в одну.
Якщо передбачається, що конверсія рент не повинна призводити до зміни фінансових наслідків для кожної сторони, то вона повинна відповідати принципу фінансової еквівалентності.
Серед різновидів конверсій можна виокремити такі: викуп ренти, відстрочка платежів, консолідація боргів.
Викуп ренти передбачає заміну одноразовим платежем усіх розподілених у часі платежів (наприклад, компенсація фонду, який створюється шляхом внесків або відрахувань). Згідно з принципом фінансової еквівалентності, викуп ренти — це виплата сучасної величини цієї ренти на даний момент.
Відстрочка платежів — це заміна одноразового платежу фінансовою рентою, тобто надання кредиту. Наприклад, у комерційному кредиті плата за відвантажену продукцію, як правило, розподіляється у часі у вигляді ренти. Для збереження принципу фінансової еквівалентності сучасну величину ренти прирівнюють до величини платежу, який замінюється (вартість відвантаженої продукції). Тоді за заданою сучасною величиною визначають розмір члена ренти та кількість платежів або термін ренти. У даному разі відстрочка платежу призведе до збільшення розміру заборгованості, але у межах, передбачених принципом фінансової еквівалентності.
Приклад 10. Вартість партії товарів 100 тис. грн., що сплачується протягом трьох років. Кредит надається під 10 % річних платежів, які вносяться кожні півроку. Покупцеві надана відстрочка на три місяці, при цьому відсотки за час відстрочки приєднуються до вартості товарів. Як здійснюватиметься погашення кредиту?
Розв’язання: Спочатку необхідно визначити вартість товарів на кінець відстрочки:
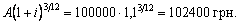 Ця сучасна величина повинна бути сплачена за три роки.
Ця сучасна величина повинна бути сплачена за три роки.
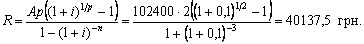 Консолідація ренти — це об’єднання кількох рент в одну. Принцип фінансової еквівалентності у даному разі передбачає виконання такої рівності:
Консолідація ренти — це об’єднання кількох рент в одну. Принцип фінансової еквівалентності у даному разі передбачає виконання такої рівності:
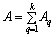 ,
,
де А — сучасна величина рент, які замінюються; Aq — сучасна величина q-ї ренти (q = 1, 2, .., k).
При об’єднанні рент можуть виникнути найрізноманітніші задачі, зокрема: а) визначення розміру члена об’єднаної ренти; б) визначення терміну об’єднаної ренти. В обох випадках повинні бути задані інші параметри рент.
Аналіз змінних потоків платежів
Змінна ренти — це рента, члени якої змінюються відповідно до якогось закону розвитку.
Нерегулярний потік платежів — це потік платежів, члени якого змінюються хаотично. Часові інтервали між двома сусідніми платежами можуть бути будь-якими. У такому разі узагальнюючі характеристики отримають лише шляхом прямого розрахунку.
Нарощена сума:
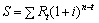 .
.
Сучасна величина:
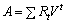 ,
,
де t — час від початку потоку платежів до моменту виплати, Rt — сума платежу (член ренти).
Змінна ренти з разовими змінами членів ренти
Загальна тривалість ренти дорівнює n. Цей строк розподілено на k періодів, у кожному член ренти постійний і дорівнює Rt.
Нарощена величина:
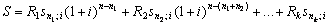 .
.
Сучасна величина:
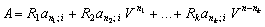 .
.
Ренти з постійним абсолютним приростом платежів
Якщо а — абсолютний приріст платежів, тобто a = Rt – Rt – 1, то сучасна величина ренти визначається за такою формулою:
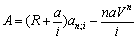 .
.
Нарощена сума ренти визначається таким чином:
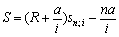 .
.
Основні категорії та поняття
Фінансова рента, або аннуїтет
Нарощена сума ренти
Сучасна величина ренти
Вічна рента
Запитання і завдання для самоконтролю
1. Що ви розумієте під таким визначенням: множину розподільних у часі платежів називають:
а) фінансовою рентою;
б) аннуїтетом;
в) потоком платежів;
г) усе викладене?
2. Яка з наведених формул є формулою нарощеної суми ренти:
а) 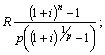 б)
б) 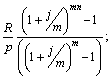 в)
в) 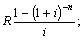 г)
г) 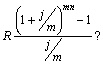
3. Що ви розумієте під визначенням: сума всіх членів послідовності платежів з нарахованими на них відсотками на кінець його строку:
а) капіталізована величини ренти;
б) нарощена сума ренти;
в) сучасна величина ренти;
г) приведена величина ренти?
4. Які з викладених нижче висловлювань неправильні:
а) член ренти — величина кожного окремого платежу;
б) відсоткова ставка — ставка, яка використовується при нарощуванні або дисконтуванні платежів, з яких складається рента;
в) період ренти — час, вимірюваний від початку фінансової ренти до кінця останнього її періоду;
г) потік платежів — це множина розподілених у часі платежів?
5. Яка з викладених нижче формул є сучасною величиною ренти:
а)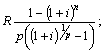 б)
б) 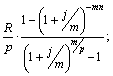 в)
в) 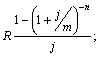 г)
г) 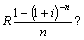 6. Під рентою розуміють:
6. Під рентою розуміють:
а) множину розподілених у часі платежів;
б) потік платежів, усі члени якого позитивні величини, а часові інтервали між двома послідовними платежами постійні;
в) потік платежів, усі члени якого позитивні величини незалежно від походження цих платежів, їх призначення і цілей;
г) множина розподілених у часі як позитивних, так і негативних платежів.
7. Що таке фінансова рента?
8. Якими параметрами описується фінансова рента?
9. Що таке нарощена сума ренти?
10. Дайте визначення сучасної величини ренти.
11. В кінці кожного кварталу на рахунок до банку перераховується сума грошей. Річна сума внесків 100 грош. од. і на ці кошти нараховуються 8 % річних. Знайти нарощену суму ренти через 10 років за умови, що відсотки на кошти на рахунку нараховуються щоквартально.
12. Необхідно визначити суму, яка потрібна для того, щоб можна було виплачувати кредиторові кожні півроку 50 грош. од. протягом 2 років, якщо на ваш рахунок у банку відсотки нараховуються щомісячно за річною ставкою 12 %.
13. Необхідно знайти нарощену суму ренти за умови, що відсотки нараховуються кожні півроку. Строк ренти 10 років. Виплата платежів один раз на кінець року по 100 грош. од. Ставка, за якою нараховуються відсотки на платежі, дорівнює 10 %.
14. Строк ренти 2 роки. Річна сума ренти становить 100 грош. од. Нарахування відсотків щомісячне за ставкою 12 % річних. Знайти сучасну величину ренти.
15. Рента виплачується 2 рази на рік. Річна сума ренти — 100 грош. од. Рента виплачуватиметься протягом двох років. Нарахування відсотків щомісячно за ставкою 12 %. Визначити нарощену суму ренти.
16. Визначити величину рівних внесків, якщо необхідно до кінця десятирічного періоду створити фонд, що дорівнюватиме 100 000 грош. од. Ставка відсотків — 10 %.
17. Строк ренти 10 років. Виплата платежів — один раз в кінці року по 100 грош. од. Ставка, за якою нараховуються відсотки по платежах, — 10 %. Визначити накопичену суму ренти.
18. Строк ренти 5 років. Нарахування відсотків у кінці року за ставкою 5 %. Член ренти дорівнює 100 грош. од. Знайти сучасну величину ренти.
19. Визначити величину щомісячних внесків на спеціальний рахунок у банку для погашення поточної заборгованості в розмірі 100 000 грош. од. Її необхідно погасити протягом двох років. Ставка відсотків — 12 %. Відсотки нараховуються щомісячно.
20. Строк ренти 10 років. Виплата платежів — один раз в кінці року по 100 грош. од. Ставка, за якою нараховуються відсотки по платежах, — 10 %. Визначити накопичену суму ренти.
21. Строк ренти 5 років. Нарахування відсотків у кінці року за ставкою 5 %. Член ренти дорівнює 100 грош. од. Знайти сучасну величину ренти.
Created/Updated: 25.05.2018
 |
|